题目内容
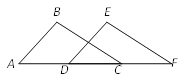
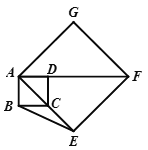
【题目】如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=![]() ,则点G 到BE的距离是( )
,则点G 到BE的距离是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据平行线的判定,可得AB与GE的关系,根据平行线间的距离相等,可得△BEG与△AEG的关系,根据根据勾股定理,可得AH与BE的关系,再根据勾股定理,可得BE的长,根据三角形的面积公式,可得G到BE的距离.
连接GB、GE,
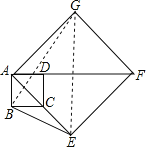
由已知可知∠BAE=45°.
又∵GE为正方形AEFG的对角线,
∴∠AEG=45°.
∴AB∥GE.
∵AE=4![]() ,AB与GE间的距离相等,
,AB与GE间的距离相等,
∴GE=8,S△BEG=S△AEG=![]() SAEFG=16.
SAEFG=16.
过点B作BH⊥AE于点H,
∵AB=2,
∴BH=AH=![]() .
.
∴HE=3![]() .
.
∴BE=2![]() .
.
设点G到BE的距离为h.
∴S△BEG=![]() BEh=
BEh=![]() ×2
×2![]() ×h=16.
×h=16.
∴h=![]() .
.
即点G到BE的距离为![]() .
.
故选A.

练习册系列答案
相关题目