题目内容
【题目】如图,在矩形ABCD中,O是对角线AC的中点.将ABCD绕点B顺时针旋转90°.旋转后的四边形为A'B′C′D',点A,C,D,O的对应点分别为A′,C',D',O’,若AB=8,BC=10,则线段CO’的长为_____.
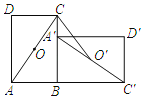
【答案】![]()
【解析】
过点O′作O′M⊥BC于点M,利用旋转的性质及三角形中线的性质可得MO′,BM的长度,从而可得CM的长度,在Rt△CO′M中,利用勾股定理即可求出答案.
解:过点O′作O′M⊥BC于点M,
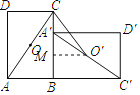
∵将ABCD绕点B顺时针旋转90°到四边形为A'B′C′D'位置,AB=8,BC=10,
∴BC′=BC=10,∠CBE=90°,BA′=AB=8,
∴O′M∥BC′,
∵O是对角线AC的中点,
∴O′是A′C′的中点,
∴MO′=![]() BC′=5,BM=A′M=
BC′=5,BM=A′M=![]() BA′=4,
BA′=4,
∴CM=BC﹣BM=10﹣4=6,
在Rt△CO′M中,CO′=![]()
故答案为:![]() .
.

练习册系列答案
相关题目