题目内容
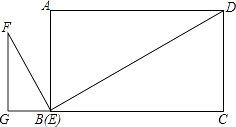
【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF,CF. 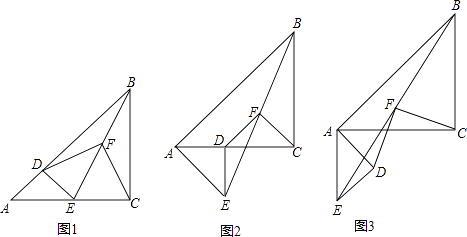
(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系(不用证明); 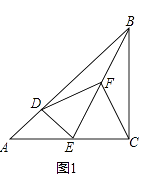
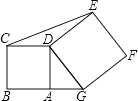
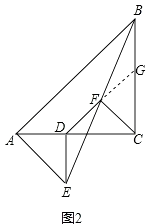
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断; 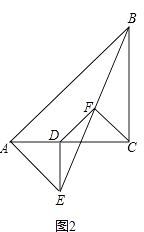
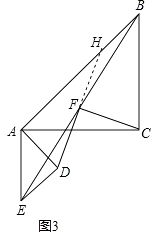
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC= ![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果). 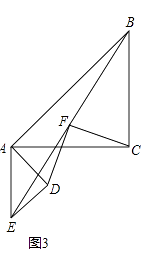
【答案】
(1)解:∵∠ACB=∠ADE=90°,点F为BE中点,
∴DF= ![]() BE,CF=
BE,CF= ![]() BE,
BE,
∴DF=CF.
∵△ABC和△ADE是等腰直角三角形,
∴∠ABC=45°
∵BF=DF,
∴∠DBF=∠BDF,
∵∠DFE=∠ABE+∠BDF,
∴∠DFE=2∠DBF,
同理得:∠CFE=2∠CBF,
∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°,
∴DF=CF,且DF⊥CF
(2)解:(1)中的结论仍然成立.
证明:如图,此时点D落在AC上,延长DF交BC于点G.
∵∠ADE=∠ACB=90°,
∴DE∥BC.
∴∠DEF=∠GBF,∠EDF=∠BGF.
∵F为BE中点,
∴EF=BF.
∴△DEF≌△GBF.
∴DE=GB,DF=GF.
∵AD=DE,
∴AD=GB,
∵AC=BC,
∴AC﹣AD=BC﹣GB,
∴DC=GC.
∵∠ACB=90°,
∴△DCG是等腰直角三角形,
∵DF=GF.
∴DF=CF,DF⊥CF
(3)解:延长DF交BA于点H,
∵△ABC和△ADE是等腰直角三角形,
∴AC=BC,AD=DE.
∴∠AED=∠ABC=45°,
∵由旋转可以得出,∠CAE=∠BAD=90°,
∵AE∥BC,
∴∠AEB=∠CBE,
∴∠DEF=∠HBF.
∵F是BE的中点,
∴EF=BF,
∴△DEF≌△HBF,
∴ED=HB,
∵AC= ![]() ,在Rt△ABC中,由勾股定理,得
,在Rt△ABC中,由勾股定理,得
AB=4,
∵AD=1,
∴ED=BH=1,
∴AH=3,在Rt△HAD中由勾股定理,得
DH= ![]() ,
,
∴DF= ![]() ,
,
∴CF= ![]()
∴线段CF的长为 ![]() .
.
【解析】(1)根据“直角三角形斜边上的中线等于斜边的一半”可知DF=BF,根据∠DFE=2∠DCF,∠BFE=2∠BCF,得到∠EFD+∠EFB=2∠DCB=90°,DF⊥BF.(2)延长DF交BC于点G,先证明△DEF≌△GCF,得到DE=CG,DF=FG,根据AD=DE,AB=BC,得到BD=BG又因为∠ABC=90°,所以DF=CF且DF⊥BF.(3)延长DF交BA于点H,先证明△DEF≌△HBF,得到DE=BH,DF=FH,根据旋转条件可以△ADH为直角三角形,由△ABC和△ADE是等腰直角三角形,AC= ![]() ,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,由DF=BF,求出得CF的值.
,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,由DF=BF,求出得CF的值.

【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题: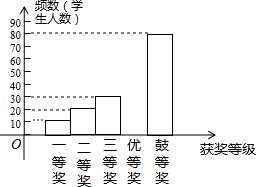
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.