题目内容
【题目】如图1，抛物线y=ax2+bx+3（a≠0）与x轴交于点A、点B（点A在点B左侧），与y轴交于点C，点D为抛物线的顶点，已知点A、点B的坐标分别为A（﹣1，0）、B（3，0）．
（1）求抛物线的解析式；
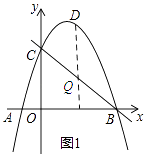
（2）在直线BC上方的抛物线上找一点P，使△PBC的面积最大，求P点的坐标；
（3）如图2，连接BD、CD，抛物线的对称轴与x轴交于点E，过抛物线上一点M作MN⊥CD，交直线CD于点N，求当∠CMN=∠BDE时点M的坐标．
【答案】
（1）
解：将A（﹣1，0）、B（3，0）两点代入y=ax2+bx+3得： 
，解得：a﹣1，b=2．
∴抛物线的表达式为：y=﹣x2+2x+3
（2）
解：由题意设P（x，﹣x2+2x+3），过点P作x轴的垂线，交直线BC于点Q．
将x=0代入抛物线的解析式得：y=3，
∴点C的坐标为（0，3）．
设直线BC的解析式为y=kx+b，将点B，C的坐标代入得： 
，
解得：k=﹣1，b=3．
∴直线CB解析式：y=﹣x+3，则Q（x，﹣x+3）
∴PQ=﹣x2+2x+3﹣（﹣x+3）=﹣x2+3x．
∴S△BCD= 
PQOB= ×（﹣x2+3x）×3=﹣ 
（x﹣ ）2+ 
．
∴当x= 时，S△BCD取最大值，
此时P（ ， 
）．
（3）
解：∵抛物线y=﹣（x﹣3）（x+1）=﹣x2+2x+3与与y轴交于点C，
∴C点坐标为（0，3），顶点（1，4），E（1，0）
∴tan∠BDE= 
= ．
①当点M在对称轴的右侧时．
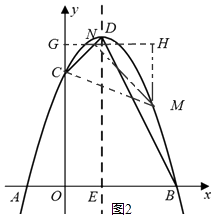
（i）作当点N在射线CD上时，如图2，过点N作y轴的垂线，垂足为G，
过点M作GN的垂线，垂足为H，则△CNG，△MNH均为等腰直角三角形．
∵∠CMN=∠BDE，
∴tan∠CMN=tan∠BDE= = 
．
∴△CNG，△MNH相似比为1：2
设CG=a，则NG=a，NH=NH=2a，
∴M（3a，3+a﹣2a），即M（3a，3﹣a），
将点M的坐标代入抛物线的解析式得：﹣（3a）2+2×3a+3=3﹣a，解得：a=0（舍去）或a= 
此时M（ 
， 
）．
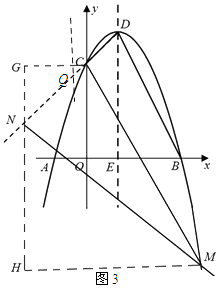
（ii）若点N在射线DC上，如图3，过点N作x轴的垂线l，分别过点M、C作GN的垂线，垂足为H、G，则△CNG，△MNH均为等腰直角三角形，
∵∠CMN=∠BDE，
∴tan∠CMN=tan∠BDE= = ，
∴△CNG与△MNH相似比为1：2
设CG=a，则NG=a，NH=NH=2a，
∴M（a，3﹣a﹣2a），即M（a，3﹣3a），
将点M的坐标代入抛物线的解析式得：﹣a2+2a+3=3﹣3a，解得：a=0（舍去）或a=5，此时M（5，12）
②当点M在对称轴左侧时．
∵∠CMN=∠BDE＜45°，
∴∠MCN＞45°，
∵抛物线左侧任意一点K，都有∠KCN＜45°，
∴点M不存在．
综上可知，点M坐标为（ ， ）或（5，12）
【解析】（1）将A（﹣1，0）、B（3，0）两点代入得到关于a、b的方程组，可求得a、b的值；（2）由题意设P（x，﹣x2+2x+3），过点P作x轴的垂线，交直线BC于点Q．先求得直线BC的解析式，则得到Q（x，﹣x+3），然后列出△BCD的面积与x的关系式，利用配方法可求得点P的横坐标以及△CBD的面积的最大值；（3）首先求得C点坐标为（0，3），顶点（1，4），E（1，0）则tan∠BDE= ．①当点M在对称轴的右侧时，作当点N在射线CD上时，如图1，过点N作y轴的垂线，垂足为G，过点M作GN的垂线，垂足为H，则△CNG，△MNH均为等腰直角三角形．设CG=a，用含a的式子表示点M的坐标，然后将点M的坐标代入抛物线的解析式可求得a的值；若点N在射线DC上，如图，过点N作x轴的垂线l，分别过点M、C作GN的垂线，垂足为H、G，则△CNG，△MNH均为等腰直角三角形，同理可求得此时a的值；②当点M在对称轴左侧时，抛物线左侧任意一点K，都有∠KCN＜45°．
