题目内容
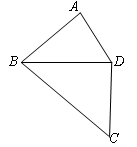
如图,在△ABC中,∠C=900,D是AC上一点,DE⊥AB于点E,若AC=8,BC=6,DE=3,则AD的长为( )


| A.3 | B.4 | C.5 | D.6 |
C
试题分析:再Rt△ABC中,先根据勾股定理求得AB的长,再证得△ABC∽△ADE,根据相似三角形的性质即可求得结果.
∵∠C=900,AC=8,BC=6
∴
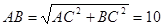
∵∠C=900,DE⊥AB,∠A=∠A
∴△ABC∽△ADE
∴
 ,即
,即 ,解得
,解得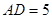
故选C.
点评:解答本题的关键是熟练掌握相似三角形的对应边成比例,注意对应字母在对应位置上.

练习册系列答案
相关题目
 的照射下在墙上形成的影子如图所示.若
的照射下在墙上形成的影子如图所示.若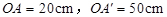 ,则这个三角尺的周长与它在墙上形成的影子的周长的比是
,则这个三角尺的周长与它在墙上形成的影子的周长的比是
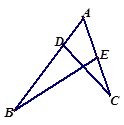
 中,AB=AC=
中,AB=AC=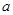 ,
, ,BD平分
,BD平分 .
.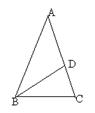
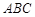 中,
中,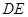 ∥
∥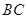 ,
,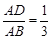 ,
, ,则
,则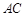 的长是( )
的长是( )
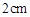


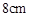
 与
与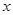 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从