题目内容
(本题12分)
如图,直线 与
与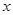 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从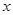 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥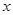 轴),并且分别与
轴),并且分别与 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.

(1)当t=1秒时,求梯形OPFE的面积;
(2)t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3)设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
如图,直线
 与
与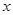 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从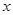 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥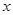 轴),并且分别与
轴),并且分别与 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)当t=1秒时,求梯形OPFE的面积;
(2)t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3)设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
(1)梯形OPFE的面积为18;(2)当t="5" (在0<t<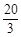 范围内)时,S最大值=50.
范围内)时,S最大值=50.
(3)作FD⊥x轴于D,则四边形OEFD为矩形.
∴FD=OE=t,AF= FD=
FD= t. 又AP=3t.
t. 又AP=3t.
当t=t1时,AF1= t1,AP1=3t1;当t=t2时,AF2=
t1,AP1=3t1;当t=t2时,AF2= t2,AP2=3t2;
t2,AP2=3t2;
∴ ,又∠A=∠A,∴△AF1P1∽△AF2P2.
,又∠A=∠A,∴△AF1P1∽△AF2P2.
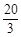 范围内)时,S最大值=50.
范围内)时,S最大值=50.(3)作FD⊥x轴于D,则四边形OEFD为矩形.
∴FD=OE=t,AF=
 FD=
FD= t. 又AP=3t.
t. 又AP=3t.当t=t1时,AF1=
 t1,AP1=3t1;当t=t2时,AF2=
t1,AP1=3t1;当t=t2时,AF2= t2,AP2=3t2;
t2,AP2=3t2;∴
 ,又∠A=∠A,∴△AF1P1∽△AF2P2.
,又∠A=∠A,∴△AF1P1∽△AF2P2.试题分析:解:设梯形OPFE的面积为S.
(1) 由直线
 与
与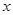 轴、
轴、 轴分别交于A、B两点
轴分别交于A、B两点∴A(20,0),B(0,20)
∴OA=OB=20,∠A=∠B=45°..
当t=1时,OE=1,AP=3,∴OP=17,EF=BE=19.
∴S=
 (OP+EF)·OE=18.
(OP+EF)·OE=18.(2) OE=t,AP=3t,∴OP=20-3t,EF=BE=20-t.
∴S=
 (OP+EF)·OE=
(OP+EF)·OE= (20-3t +20-t)·t =-2t2+20t=-2(t-5)2+50.
(20-3t +20-t)·t =-2t2+20t=-2(t-5)2+50.∴当t="5" (在0<t<
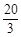 范围内)时,S最大值="50."
范围内)时,S最大值="50." 

|
 (3) 作FD⊥x轴于D,则四边形OEFD为矩形.
(3) 作FD⊥x轴于D,则四边形OEFD为矩形. ∴FD=OE=t,AF=
∴FD=OE=t,AF= FD=
FD= t. 又AP=3t.
t. 又AP=3t.当t=t1时,AF1=
 t1,AP1=3t1;当t=t2时,AF2=
t1,AP1=3t1;当t=t2时,AF2= t2,AP2=3t2;
t2,AP2=3t2;∴
 ,又∠A=∠A,∴△AF1P1∽△AF2P2.
,又∠A=∠A,∴△AF1P1∽△AF2P2.点评:难题较高。本题考查学生对梯形面积公式的计算,相似三角形判定及动点和动直线作用下图形变化的理解,找出相对应的变量,结合上下题之间能使用的关系式进行计算。要能够在众多条件中准确找出对应所需的信息。

练习册系列答案
相关题目
 =
= 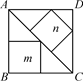



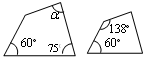
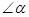 的度数是
的度数是