题目内容
如图,在四边形ABCD中,DC∥AB,BD平分∠ADC,∠ADC=60°,过点B作BE⊥DC,过点A作AF⊥BD,垂足分别为E、F,连接EF判断△BEF的形状,并说明理由


三角形BFE是等边三角形
试题分析:利用直角三角形斜边上的中线等于斜边的一半求得DF=BF=EF,然后利用∠DBE=60°根据有一个角是60°的等腰三角形是等边三角形证得三角形BEF为等边三角形即可
试题解析:等边三角形,理由如下:
∵∠ADC=60°,BD平分∠ADC
∴∠ADE=∠BDE=30° 1分
∵DC∥AB
∴∠ABD=∠BDC 1分
∵AF⊥BD
∴DF=BF 1分
∵BE⊥DC
∴DF=BF=EF 1分
∴∠FDE=∠FED=30° 1分
∴∠BFE=∠BDE+∠FED=60° 1分
∴三角形BFE是等边三角形 2分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




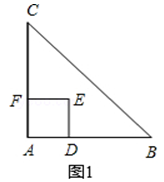

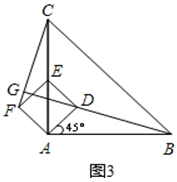
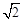 时,求线段FG的长.
时,求线段FG的长.