Question

已知：如图,E为正方形ABCD的边BC延长线上的点,F是CD边上一点,且CE=CF,连接DE、BF．

（1）求证：DE=BF；
（2）判断BF与DE的位置关系,并说明理由.

Answer 1

证明见解析.

试题分析：根据已知利用边角边得出△ABF≌△CBE,进而求出∠ECB+∠CFH=90°即可．
试题解析：（1）∵正方形ABCD,
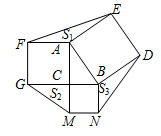
∴AB=CB,∠ABC=∠CBE=90°,
∵BE=BF,
,
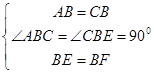∴△ABF≌△CBE （SAS）,
∴AF=CE,
（2）延长AF交CE于点H．
 
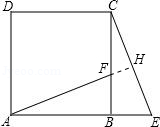
∵△ABF≌△CBE
∴∠FAB=∠ECB,
∵∠FAB+∠AFB=90°,
又∵∠AFB=∠CFH,
∴∠ECB+∠CFH=90°,
∴∠CHF=90°,
∴AF⊥CE．