题目内容
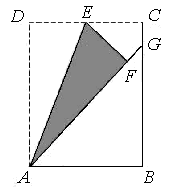
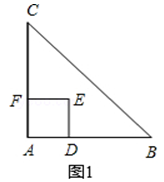
如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
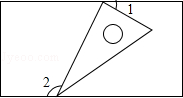
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.

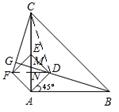
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
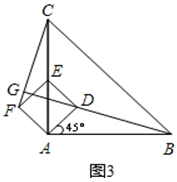
①求证:BD⊥CF;
②当AB=4,AD=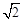 时,求线段FG的长.
时,求线段FG的长.

(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.

(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.

①求证:BD⊥CF;
②当AB=4,AD=
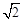 时,求线段FG的长.
时,求线段FG的长.(1) BD=CF成立,证明见解析;(2)①证明见解析;②FG=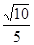 .
.
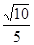 .
.试题分析:(1)证明线段相等的常用方法是三角形的全等,直观上判 断BD=CF,而由题目条件,旋转过程中出
现了两个三角形△BAD和△CAF,并且包含了要证明相等的两条线段BD和CF,∵△ABC是等腰直角三角形,∴AB=AC,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,只差夹角相等,在Rt△BAC中,∠BAD+∠DAC=90°,∠CAF+∠DAC="90°," ∴∠BAD="∠CAF," ∴△BAD≌△CAF, BD=CF.(2)①要证明BD⊥CF,只要证明∠BGC=90°,即∠GBC+∠BCG=∠GBC+∠ACF+∠ACB=90°,在Rt△BAC中,∠ABC+
∠ACB=∠ABG+∠GBC+∠BCA=90°,有(1)知,∠ACF=∠ABG,所以∠GBC+∠ACF+∠ACB=∠GBC+
∠ABG +∠ACB =90°,所以BD⊥CF.②求线段的方法一般是三角形的全等和勾股定理,题目中没有和FG直接相关的线段,而CG从已知条件中又无法求出,所以需要作辅助线,连接FD,交AC于点N, 在正方形ADEF中,AD=DE=
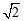 , AN="1," CN=3,由勾股定理CF=
, AN="1," CN=3,由勾股定理CF=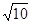 ,设FG=x,CG=
,设FG=x,CG=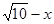 ,在Rt△FGD中,∵FD=2,∴GD=
,在Rt△FGD中,∵FD=2,∴GD=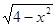 ,∵在Rt△BCG中,
,∵在Rt△BCG中,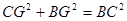 ,
,∴
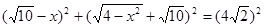 ,解之得FG=
,解之得FG=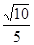 .
.试题解析:②解法一:
如图,连接FD,交AC于点N,

∵在正方形ADEF中,AD=DE=
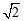 ,
,∴AN=FN=
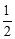 AE=1,FD=2,
AE=1,FD=2,∵在等腰直角△ABC 中,AB=4,∴CN=AC-AN=3,
∴在Rt△FCN中,
 ,
,∵△BAD≌△CAF(已证),∴BD=CF=
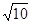 ,
,设FG=
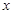 ,在Rt△FGD中,∵FD=2,∴GD=
,在Rt△FGD中,∵FD=2,∴GD=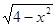 ,
,∵CF=
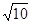 ,∴CG=
,∴CG=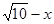 ,
,∵在等腰直角△ABC 中,AB=AC=4,
∴
 ,
,∵在Rt△BCG中,
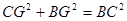 ,
,∴
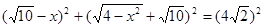 ,
, 整理,得
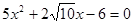 ,
,解之,得
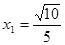 ,
,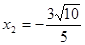 (不合题意,故舍去)
(不合题意,故舍去)∴FG=
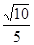 .
.解法二:
如图,连接FD,交AC于点N;连接CD,
同解法一,可得:DG=
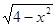 ,CG=
,CG=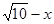 ,
, 易证△ACD≌△ABD(SAS),可得CD=BD=
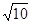 ,
, 在Rt△CGD中,
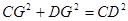 ,即
,即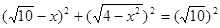
解之,得
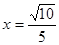 ,故FG=
,故FG=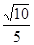 .
.
练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目


 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题: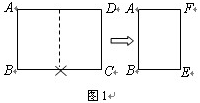


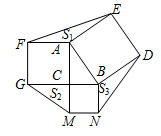
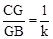 ,则
,则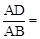 (用含k的代数式表示).
(用含k的代数式表示).