题目内容
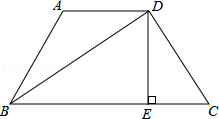
如图,在□ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P.

(1)求证:△ABE≌△DCF;
(2)当∠P满足什么条件时,四边形BECF是菱形?证明你的结论.

(1)求证:△ABE≌△DCF;
(2)当∠P满足什么条件时,四边形BECF是菱形?证明你的结论.
见解析
试题分析:(1)因为ABCD是平行四边形,所以对角相等,对边相等。而E、F又是对边中点,利用“SAS” 即可证明△ABE≌△DCF
(2)∠P=90°时,四边形BECF是菱形。
要使四边形BECF是菱形,只要邻边相等即可,也就是说只要满足BE=EC即可,假设BE=EC,由于AE=EC,所以有AE=BE,BE=CE,所以∠ABE=∠BAE,∠EBC=∠ECB,而∠ABE+∠BAE+∠EBC+∠ ECB=180°(△ABC内角和).所以2∠ABE+2∠EBC=180°,所以∠ABE+∠EBC=90°,即∠ABC=90°,由于AB//CP,AP//BC,所以四边形BAPC是平行四边形,所以∠P=∠ABC=90º.
试题解析:
(1)证明:∵ABCD是平行四边形,
∴∠A=∠D,AB=CD,BD=AC
∵E、F分别为AC,BD中点
∴AE=FD
在△ABE和△DCF中,
AB=CD,∠A=∠D,AE=FD
∴△ABE≌△DCF
(2)解:问题可知使四边形BECF是菱形,
∴BE=EC
又∵AE=EC
∴∠EBC=∠ECB
BE=AE
∴∠A=∠ABE
∵∠A+∠ABE+∠EBC+∠ECB=180º
∴2∠ABE+2∠EBC=180º
∴∠ABE+∠EBC=90º
∴∠ABC=90º
又∵AB//CP,AP//BC
∴四边形BAPC是平行四边形
∴∠P=∠ABC=90º
即∠P=90º时,四边形BECF是菱形

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目


 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题: