题目内容
若矩形ABCD的对角线长为10,点E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长是 .
20
试题分析:∵矩形ABCD的对角线长为10,
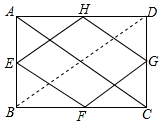
∴AC=BD=10。
∵点E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF=HG=
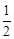 AC=
AC=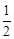 ×10=5,EH=GF=
×10=5,EH=GF=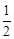 BD=
BD=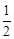 ×10=5。
×10=5。∴四边形EFGH的周长为EF+FG+GH+HE=5+5+5+5=20。

练习册系列答案
相关题目
题目内容

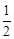 AC=
AC=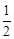 ×10=5,EH=GF=
×10=5,EH=GF=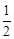 BD=
BD=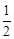 ×10=5。
×10=5。