题目内容
在菱形ABCD中,∠B=60°,点E、F分别在AB、AD 上.
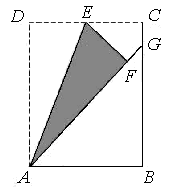
(1)如图1,若点E、F分别为AB、AD的中点,问点C在线段EF的垂直平分线上吗?请直接回答,不需要说明理由.

答: .
(2)如图2,若点E、F分别在AB、AD上,且BE=AF,问点C在线段EF的垂直平分线上吗?请说明你的理由.

(1)如图1,若点E、F分别为AB、AD的中点,问点C在线段EF的垂直平分线上吗?请直接回答,不需要说明理由.

答: .
(2)如图2,若点E、F分别在AB、AD上,且BE=AF,问点C在线段EF的垂直平分线上吗?请说明你的理由.

(1)点C在线段EF的垂直平分线上;(2)点C在线段EF的垂直平分线上,理由见解析.
试题分析:(1)根据菱形的性质知道菱形的对角线平分对角,而点E、F分别为AB、AD的中点,容易得到AE=AF,根据等腰三角形性质即可得到结论;
(2)点C在线段EF的垂直平分线上.首先根据菱形的性质和∠B=60°可以得到△ABC和△ADC都为等边三角形,然后连接CE、CF,利用已知条件可以证明△ACF≌△BCE,再利用全等三角形的性质得到CF=CE,最后利用线段的垂直平分线的性质即可得到结论.
试题解析:
(1)点C在线段EF的垂直平分线上;
(2)点C在线段EF的垂直平分线上,
∵四边形ABCD是菱形且∠B=60°,
∴△ABC和△ADC都为等边三角形,
∴AC=BC,∠FAC=EBC=60°,
连接CE、CF,
在△ACF和△BCE中,
∵AF=BE,∠FAC=∠EBC,AC=BC,
∴△ACF≌△BCE,
∴CF=CE,
∴点C在线段EF的垂直平分线上.

练习册系列答案
相关题目



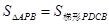

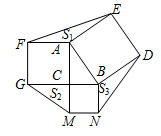

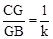 ,则
,则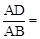 (用含k的代数式表示).
(用含k的代数式表示).