题目内容
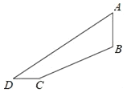
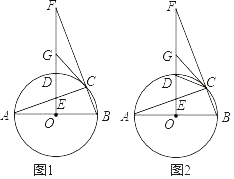
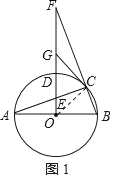
【题目】如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BCBF;
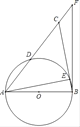
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
【答案】(1)CG与⊙O相切,理由见解析;(2)见解析;(3)DE=2
【解析】
(1)连接CE,由AB是直径知△ECF是直角三角形,结合G为EF中点知∠AEO=∠GEC=∠GCE,再由OA=OC知∠OCA=∠OAC,根据OF⊥AB可得∠OCA+∠GCE=90°,即OC⊥GC,据此即可得证;
(2)证△ABC∽△FBO得![]() ,结合AB=2BO即可得;
,结合AB=2BO即可得;
(3)证ECD∽△EGC得![]() ,根据CE=3,DG=2.5知
,根据CE=3,DG=2.5知![]() ,解之可得.
,解之可得.
解:(1)CG与⊙O相切,理由如下:
如图1,连接CE,
∵AB是⊙O的直径,
∴∠ACB=∠ACF=90°,
∵点G是EF的中点,
∴GF=GE=GC,
∴∠AEO=∠GEC=∠GCE,
∵OA=OC,
∴∠OCA=∠OAC,
∵OF⊥AB,
∴∠OAC+∠AEO=90°,
∴∠OCA+∠GCE=90°,即OC⊥GC,
∴CG与⊙O相切;
(2)∵∠AOE=∠FCE=90°,∠AEO=∠FEC,
∴∠OAE=∠F,
又∵∠B=∠B,
∴△ABC∽△FBO,
∴![]() ,即BOAB=BCBF,
,即BOAB=BCBF,
∵AB=2BO,
∴2OB2=BCBF;
(3)由(1)知GC=GE=GF,
∴∠F=∠GCF,
∴∠EGC=2∠F,
又∵∠DCE=2∠F,
∴∠EGC=∠DCE,
∵∠DEC=∠CEG,
∴△ECD∽△EGC,
∴![]() ,
,
∵CE=3,DG=2.5,
∴![]() ,
,
整理,得:DE2+2.5DE﹣9=0,
解得:DE=2或DE=﹣4.5(舍),
故DE=2.