题目内容
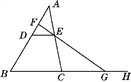
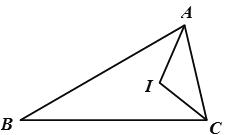
【题目】如图，在△ABC中，∠BAC．∠BCA的平分线交于点I，若∠ACB=75°，AI=BC－AC，则∠B的度数为（ ）
A.30°B.35°C.40°D.45°
【答案】B
【解析】
在BC上取一点D，使得DC=AC，连接BI，DI，结合已知条件得出DB=AI，根据全等三角形的判定可证的△ACI≌△DCI，从而得到BD=ID，设∠IBD=x，利用题目条件表示出∠ABC、∠BAC，最后根据三角形的内角和等于180°即可得出结果．
解：如图所示，在BC上取一点D，使得DC=AC，连接BI，DI
∵AI=BC－AC
∴AI=BD
∵IC是∠ACB的角平分线，AI是∠BAC的角平分线
∴IB是∠ABC的角平分线
∴∠ACI=∠ICB，∠BAI=∠IAC，∠ABI=∠IBC
在△ACI和△ICD中
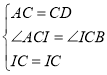
∴△ACI≌△DCI（SAS）
∴AI=ID=BD，∠IAC=∠IDC
∴△IDB是等腰三角形
∴∠IBD=∠BID
∵∠IDC=∠IBD+∠BID=2∠IBD
设∠IBD=x，则∠ABC=2x，∠IAC=2x
则：2x+4x+75°=180°
解得：x=17.5°
∴∠ABC=2×17.5°=35°
故选：B．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
