题目内容
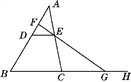
【题目】如图，点D，E分别在AB，AC上，DE∥BC，F是AD上一点，FE的延长线交BC的延长线于点G.求证：
(1)∠EGH>∠ADE；
(2)∠EGH＝∠ADE＋∠A＋∠AEF.
【答案】（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据三角形的外角性质得出∠EGH>∠B，再根据平行线的性质得出∠B=∠ADE，即可得出答案；（2）根据三角形的外角性质得出∠BFE=∠A+∠AEF，∠EGH=∠B+∠BFE，根据平行线的性质得出∠B=∠ADE，即可得出答案．
试题解析：
证明：(1)因为∠EGH是△FBG的外角，
所以∠EGH>∠B.
又因为DE∥BC，
所以∠B＝∠ADE.
所以∠EGH>∠ADE.
(2)因为∠BFE是△AFE的外角，
所以∠BFE＝∠A＋∠AEF.
因为∠EGH是△BFG的外角，
所以∠EGH＝∠B＋∠BFE.
所以∠EGH＝∠B＋∠A＋∠AEF.
又因为DE∥BC，所以∠B＝∠ADE，
所以∠EGH＝∠ADE＋∠A＋∠AEF.
练习册系列答案
阅读快车系列答案
相关题目
