Question

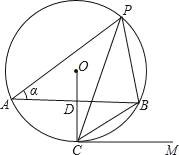
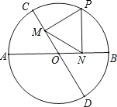
【题目】如图，AB、CD是⊙O的直径，P为上一个动点(不与B、C重合)，PM、PN分别垂直CD、AB，垂足分别为点M、N.若∠AOC=60°，OA=4，则MN的长为________.

Answer 1

【答案】

【解析】

如图所示，延长PN交圆于点E，延长PM交圆于点F，连接EF、OE、OF，作OH⊥EF于H．根据垂径定理，PN=NE，PM=MF，推出MN∥EF且MN=EF，由∠MON=120°，∠PNO=∠PMO=90°，推出∠P=60°，推出弦EF的长为定值，

解：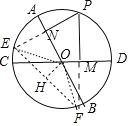
如图所示，延长PN交圆于点E，延长PM交圆于点F，连接EF、OE、OF，作OH⊥EF于H．根据垂径定理，PN=NE，PM=MF，
∴MN∥EF且MN=EF，
∵∠MON=120°，∠PNO=∠PMO=90°，
∴∠P=60°，
∴弦EF的长为定值，MN的长也为定值，
在Rt△EOH中，易知∠EOH=60°，∵OE=OA=4，
∴EH=OEsin60°=，
∴EF=4，
∴MN=EF=2，
故答案为2．