题目内容
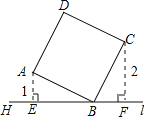
【题目】如图所示,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是AE=1,CF=2,则EF长为 .
【答案】3
【解析】
试题分析:根据正方形的性质得AB=BC,∠ABC=90°,再根据等角的余角相等得到∠EAB=∠FBC,则可根据“ASA”判断△ABE≌△BCF,所以BE=CF=2,进而求出EF的长.
解:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥BE,CF⊥BF,
∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,∠ABE+∠FBC=90°,
∴∠EAB=∠FBC,
在△ABE和△BCF中,
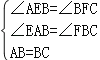 ,
,
∴△ABE≌△BCF(ASA),
∴BE=CF=2,AE=BF=1,
∴EF=BE+BF=3.
故答案为3.

练习册系列答案
相关题目