��Ŀ����
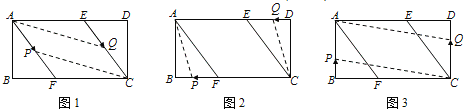
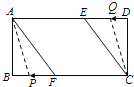
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
��1����ͼ1������AF��CE����֤�ı���AFCEΪ���Σ�����AF�ij���
��2����ͼ2������P��Q�ֱ��A��C����ͬʱ����������AFB����CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У�
����֪��P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬��A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
������P��Q���˶�·�̷ֱ�Ϊa��b����λ��cm��ab��0������֪A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���a��b�����������ϵʽ��

���𰸡���1��֤����������AF=5cm��
��2������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]() �룮
�룮
��a��b�����������ϵʽ��a+b=12��ab��0����
��������
��1����֤���ı���AFCEΪƽ���ı��Σ��ٸ��ݶԽ����ഹֱƽ�ֵ�ƽ���ı��������������ж������ݹ��ɶ����������AF�ij���
��2����������ۿ�֪����P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴��.
��1��֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���CAD=��ACB����AEF=��CFE��
��EF��ֱƽ��AC������ΪO��
��OA=OC��
���AOE�ա�COF��
��OE=OF��
���ı���AFCEΪƽ���ı��Σ�
�֡�EF��AC��
���ı���AFCEΪ���Σ�
�����εı߳�AF=CF=xcm����BF=��8��x��cm��
��Rt��ABF��AB=4cm��
�ɹ��ɶ�����42+��8��x��2=x2��
���x=5��
��AF=5cm��
��2������Ȼ��P����AF��ʱ��Q����CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
ͬ��P����AB��ʱ��Q����DE��CE�ϣ�Ҳ���ܹ���ƽ���ı��Σ�
���ֻ�е�P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��PC=QA��
�ߵ�P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC=5t��QA=12��4t��
��5t=12��4t��
���![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]() �룮
�룮
��������ã���A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����P��Q�ڻ���ƽ�еĶ�Ӧ���ϣ�
�����������
i����ͼ1����P����AF�ϡ�Q����CE��ʱ��AP=CQ����a=12��b����a+b=12��
ii����ͼ2����P����BF�ϡ�Q����DE��ʱ��AQ=CP����12��b=a����a+b=12��
iii����ͼ3����P����AB�ϡ�Q����CD��ʱ��AP=CQ����12��a=b����a+b=12��
����������a��b�����������ϵʽ��a+b=12��ab��0����