Question

【题目】如图，点A1（1，1）在直线y=x上，过点A1分别作y轴、x轴的平行线交直线y= x于点B1 ， B2 ， 过点B2作y轴的平行线交直线y=x于点A2 ， 过点A2作x轴的平行线交直线y= x于点B3 ， …，按照此规律进行下去，则点An的横坐标为 ．

Answer 1

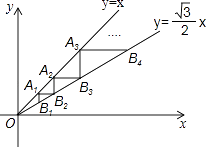
【答案】
【解析】解：∵AnBn+1∥x轴，

∴tan∠AnBn+1Bn= ．

当x=1时，y= x= ，

∴点B1的坐标为（1， ），

∴A1B1=1﹣ ，A1B2= = ﹣1．

∵1+A1B2= ，

∴点A2的坐标为（ ， ），点B2的坐标为（ ，1），

∴A2B2= ﹣1，A2B3= = ﹣ ，

∴点A3的坐标为（ ， ），点B3的坐标为（ ， ）．

同理，可得：点An的坐标为（ ， ）．

所以答案是： ．

【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．