题目内容
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A.S3>S4>S6
B.S6>S4>S3
C.S6>S3>S4
D.S4>S6>S3
【答案】B
【解析】解:设正六边形的边长为a,如图所示,
则正△ABC的边长为2a,正方形ABCD的边长为 ![]() .
.
如图(1),过A作AD⊥BC,D为垂足;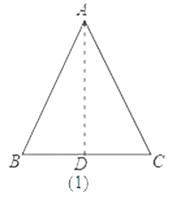
∵△ABC是等边三角形,BC=2a,
∴BD=a,由勾股定理得,AD= ![]() =
= ![]() =
= ![]() a,
a,
∴S3=S△ABC= ![]() BCAD=
BCAD= ![]() ×2a×
×2a× ![]() a=
a= ![]() a2≈1.73a2 .
a2≈1.73a2 .
如图(2),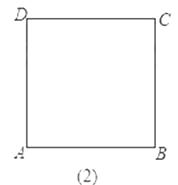
∵四边形ABCD是正方形,
∴AB= ![]() ,
,
∴S4=S□ABCD=AB2= ![]() ×
× ![]() =
= ![]() a2≈2.25a2 .
a2≈2.25a2 .
如图(3),过O作OG⊥BC,G为垂足,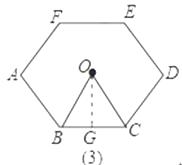
∵六边形ABCDEF是正六边形,
∴∠BOC= ![]() =60°,
=60°,
∴∠BOG=30°,OG= ![]() =
= ![]() =
= ![]() a.
a.
∴S△BOC= ![]() ×
× ![]() a×a=
a×a= ![]() a2 ,
a2 ,
∴S6=6S△BOC=6× ![]() a=
a= ![]() a2≈2.59a2 .
a2≈2.59a2 .
∵2.59a2>2.25a2>1.73a2 .
∴S6>S4>S3 .
故答案为:B.
根据正六边形的边长和半径相等,因此设正六边形的边长为a,再根据正六边形、正三角形、正方形的周长相等,用含a的代数式分别表示出正三角形和正方形的边长,然后分别求正六边形、正三角形、正方形的面积,比较它们的面积大小,即可得出答案。

练习册系列答案
相关题目