题目内容
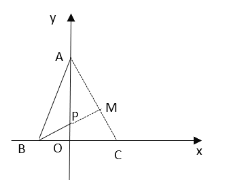
【题目】如图,在平面直角坐标系中,点 A 在 y 轴正半轴上点 B 在 x 轴负半轴上,且 AB=2,∠BAO=15°,点 P 是线段OA 上的一个动点,则 PB ![]() PA 的最小值为_____________.
PA 的最小值为_____________.

【答案】![]() .
.
【解析】
在y轴右侧取∠OAC=30°,过点P作PM⊥AC,利用含30°的直角三角形的性质求得PM=![]() ,然后利用两点之间线段最短分析得出当点B,P,M三点共线时PB PM最小,即BM的长,从而利用等腰直角三角形的性质求解.
,然后利用两点之间线段最短分析得出当点B,P,M三点共线时PB PM最小,即BM的长,从而利用等腰直角三角形的性质求解.
解:在y轴右侧取∠OAC=30°,过点P作PM⊥AC
∵在Rt△OAC中,∠OAC=30°
∴PM=![]()
∴PB ![]() PA= PB PM
PA= PB PM
∴当点B,P,M三点共线时PB PM最小,即BM的长
又∵∠BAO=15°,∠OAC=30°,PM⊥AC
∴在Rt△ABM中,∠BAM=45°
∴BM=![]()
则PB ![]() PA 的最小值为
PA 的最小值为![]()
故答案为:![]() .
.

练习册系列答案
相关题目






