题目内容
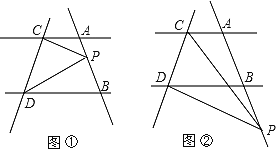
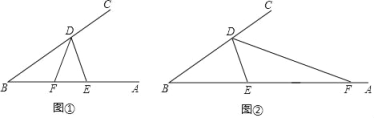
【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.
【答案】(1)见解析;(2)EF=DE+BD,证明见解析.
【解析】
(1)如图①,在BA上截取EG=DE,连接DG,得到∠EDG=∠EGD,根据三角形外角的性质和角平分线的定义即可得到结论;
(2)在BA上截取EG=DE,连接DG,则∠EDG=∠EGD,根据三角形外角的性质和角平分线的定义即可得到结论.
(1)如图①,在BA上截取EG=DE,连接DG,
则∠EDG=∠EGD,
∵∠DEB=∠EDG+∠EGD=2∠EGD,
∵∠DEB=2∠B,
∴∠B=∠DGB,
∴BD=DG,
∵DF平分∠BDE,
∴∠BDF=∠EDF,
∵∠DFE=∠B+∠BDF,∠FDG=∠FDE+∠EDG,
∴∠DFG=∠FDG,
∴DG=GF,
∴FG=BD,
∵FG=EF+AE,
∴BD=DE+EF;
(2)如图②在BA上截取EG=DE,连接DG,
则∠EDG=∠EGD,
∵∠DEB=∠EDG+∠EGD=2∠EGD,
∵∠DEB=2∠B,
∴∠B=∠DGB,
∴BD=DG,
∵DF平分∠CDE,
∴∠CDF=∠EDF,
∵∠DFE=∠CDF﹣∠B,∠GDF=∠EDF﹣∠EDG,
∴∠GDF=∠DFG,
∴DG=FG,
∴GF=BD,
∵EF=EG+GF,
∴EF=DE+BD.


练习册系列答案
相关题目