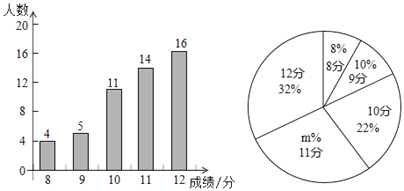
题目内容
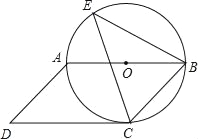
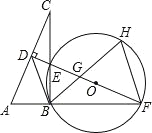
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线相交于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
(1)求证:△HGF∽△HFB;
(2)求证:BD=![]() EF;
EF;
(3)连接HE,若AB=2,求△HEF的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)直接利用角平分线的定义结合相似三角形的判定方法得出答案;
(2)首先得出△ABC≌△EBF(ASA),进而得出BD=![]() AC=
AC=![]() EF;
EF;
(3)结合勾股定理得出EF2=BE2+BF2=22+(2+2![]() )2=16+8
)2=16+8![]() ,进而得出S△HEF=
,进而得出S△HEF=![]() HFHE=
HFHE=![]() HE2,求出答案即可.
HE2,求出答案即可.
(1)证明:∵BH为∠EBF的平分线,
∴∠EBH=∠FBH,
又∵∠EBH=∠EFH,
∴∠EFH=∠FBH,
而∠BHF=∠BHF,
∴△HGF∽△HFB;
(2)证明:∵∠ABC=90°,
∴∠EBF=∠ABC=90°,
∵∠BFE+∠A=90°,∠C+∠A=90°,
∴∠BFE=∠C,
在△ABC和△EBF中
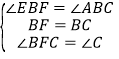 ,
,
∴△ABC≌△EBF(ASA),
∴AC=EF,
∵∠ABC=90°,D为AC中点,
∴BD=![]() AC=
AC=![]() EF;
EF;
(3)解:连接EA,EH,由于DF为垂直平分线,
∴CE=EA=![]() AB=2
AB=2![]() ,BF=BC=2+2
,BF=BC=2+2![]() ,
,
∴EF2=BE2+BF2=22+(2+2![]() )2=16+8
)2=16+8![]() ,
,
又∵BH为∠EBF平分线,
∴∠HEF=∠HFE=45°,
∴HE=HF且HE2+HF2=EF2,
∴HE2=HF2=8+4![]() ,
,
∴在等腰Rt△HEF中,S△HEF=![]() HFHE=
HFHE=![]() HE2=4+2
HE2=4+2![]() .
.

练习册系列答案
相关题目