Question

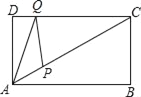
【题目】如图，矩形ABCD中，AD=5，∠CAB=30°，点P是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是___________．

Answer 1

【答案】5

【解析】

作点A关于直线CD的对称点E，作EP⊥AC于P，交CD于点Q，此时QA+QP最短，由QA+QP=QE+PQ=PE可知，求出PE即可解决问题．

解：作点A关于直线CD的对称点E，作EP⊥AC于P，交CD于点Q．

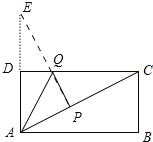
∵四边形ABCD是矩形，

∴∠ADC=90°，

∴DQ⊥AE，∵DE=AD，

∴QE=QA，

∴QA+QP=QE+QP=EP，

∴此时QA+QP最短（垂线段最短），

∵∠CAB=30°，

∴∠DAC=60°，

在Rt△APE中，∵∠APE=90°，AE=2AD=10，

∴EP=AEsin60°=10×=5．

故答案为5．