题目内容
【题目】在一次数学课上，王老师在黑板上画出一幅图，并写下了四个等式：
①
，②
，③
，④
．
（1）上述四个条件中，由哪两个条件可以判定
是等腰三角形？用序号写出所有成立的情形．
（2）请选择(1)中的一种情形，写出证明过程．
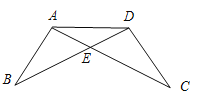
【答案】（1）①③、①④、②③、②④；（2）选择①③，证明见解析
【解析】
（1）只要能证明△ABE≌△DCE的条件都可以，所以可以根据全等三角形的判定方法来写出答案；
（2）选择一种证明△ABE≌△DCE，可得到AE＝DE，可证明△AED为等腰三角形．
（1）①③、①④、②③、②④都可以证明△ABE≌△DCE，可得到AE＝DE，可判定△AED为等腰三角形；
（2）选择①③，证明如下：
在△ABE和△DCE中，
，
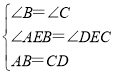∴△ABE≌△DCE（AAS），
∴AE＝DE，
∴△AED为等腰三角形．
练习册系列答案
相关题目
【题目】苏州太湖养殖场计划养殖蟹和贝类产品，这两个品种的种苗的总投放量只有50吨，根据经验测算，这两个品种的种苗每投放一吨的先期投资，养殖期间的投资以及产值如下表（单位：万元/吨）
品种 | 先期投资 | 养殖期间投资 | 产值 |
贝类产品 | 0.9 | 0.3 | 0.33 |
蟹产品 | 0.4 | 1 | 2 |
养殖场受经济条件的影响，先期投资不超过36万元，养殖期间的投资不超过29万元，设贝类的种苗投放量为x吨，
（1）求x的取值范围；
（2）设这两个品种产出后的总产值为y（万元），试写出y与x之间的函数关系式，并求出当x等于多少时，y有最大值？最大值是多少？
