题目内容
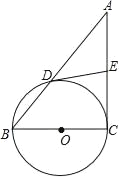
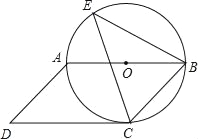
【题目】如图,四边形ABCD是平行四边形,以边AB为直径的⊙O经过点C,E是⊙O上的一点,且∠BEC=45°.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若BE=8cm,sin∠BCE=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)相切,详见解析;(2)⊙O的半径为5 cm.
【解析】
(1)连接OC,根据圆周角定理得到∠BOC=2∠BEC=90°,再根据平行四边形的性质可得AB∥CD,则∠OCD=∠BOC=90°,然后根据切线的判定定理即可得到CD与⊙O相切;
(2)连接AE,根据圆周角定理及其推论得∠AEB=90°,∠EAB=∠BCE,而sin∠BCE=![]() ,则sin∠EAB=
,则sin∠EAB=![]() ,根据三角函数的定义易求出AB,即可得到圆的半径.
,根据三角函数的定义易求出AB,即可得到圆的半径.
解:(1)相切.理由如下:
连接OC,如图,
∵∠BEC=45°,
∴∠BOC=90°,
又∵四边形ABCD是平行四边形,
∴AB∥CD.
∴∠OCD=∠BOC=90°,
∴OC⊥CD.
∴CD为⊙O的切线;
(2)连接AE,如图,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵∠EAB=∠BCE,sin∠BCE=![]() ,
,
∴sin∠EAB=![]() ,
,
∴![]() =
=![]() ,
,
∵BE=8,
∴AB=10,
∴AO=![]() AB=5,
AB=5,
∴⊙O的半径为5 cm.

练习册系列答案
相关题目
【题目】如图,已知△ABC的三个顶点坐标如下表:
(1)将下表补充完整,并在直角坐标系中,画出△A′B′C′;
(x,y) | (2x,2y) |
A(2,1) | A′(4,2) |
B(4,3) | B′( ) |
C(5,1) | C′( ) |
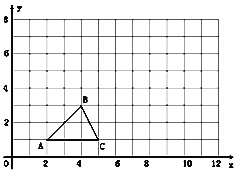
(2)观察两个三角形,可知△ABC∽△A′B′C′两个三角形的是以原点为位似中心的位似三角形,△ABC与△A′B′C′的位似比为 .