题目内容
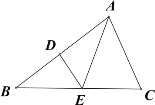
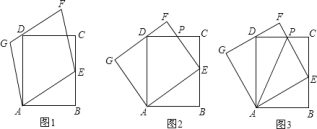
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,
,![]() .
.
(1)求证:![]() 是等腰三角形.
是等腰三角形.
(2)若![]() 为等边三角形,求
为等边三角形,求![]() 的度数.
的度数.

【答案】(1)证明见解析;(2)∠A=60°.
【解析】
(1)证明△DBE≌△CEF得到DE=EF,即可得到结论;
(2)由已知得到∠DEF=60°,根据外角的性质及△DBE≌△CEF得到∠DEF+∠CEF=∠B+∠BDE,求得∠B =∠DEF=60°,再根据AB=AC即可求出![]() 的度数.
的度数.
(1)证明:∵AB=AC,∴∠B=∠C.
在△DBE 和△CEF 中,
∴△DBE≌△ECF.
∴DE=EF.
∴△DEF 是等腰三角形.
(2)∵△DEF为等边三角形,
∴∠DEF=60°.
∵△DBE≌△CEF,∴∠BDE=∠CEF.
∵∠DEF+∠CEF=∠B+∠BDE,∴∠B =∠DEF=60°.
∴∠C=∠B=60°.
∴∠A=180°-∠B-∠C=60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目