题目内容
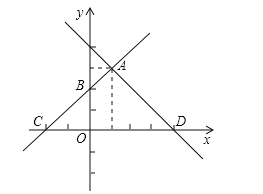
【题目】如图正比例函数y=2x的图像与一次函数 
的图像交于点A（m,2）,一次函数的图象经过点B（-2，-1）与y轴交点为C与x轴交点为D.
（1）求一次函数的解析式；
（2）求
的面积。
【答案】（1）一次函数的解析式为
；（2）1.
【解析】（1）首先根据正比例函数解析式求得m的值，再进一步运用待定系数法求得一次函数的解析式；
（2）根据（1）中的解析式，令y=0求得点C的坐标，从而求得三角形的面积.
解：（1）由题可得，把点A（m,2）代入正比例函数y=2x 得
2＝2m
m=1
所以点A（1,2）
因为一次函数图象又经过点B（-2,-1），所以
解方程组得
这个一次函数的解析式为
（2）因为一次函数图象与x轴的交点为D，
所以点D的坐标为（-1,0）
因为
的底为OD=1,高为A点的纵坐标2
所以
“点睛”此题综合考查了待定系数法求函数解析式、直线与坐标轴的交点的求法，关键是根据正比例函数解析式求得m的值.
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】为举办校园文化艺术节，甲、乙两班准备给合唱同学购买演出服装(一人一套)，两班共92人(其中甲班比乙班人多，且甲班不到90人)，下面是供货商给出的演出服装的价格表：
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装，那么一共应付5020元．
(1)甲、乙两班联合起来给每位同学购买一套服装，比单独购买可以节省多少钱？
(2)甲、乙两班各有多少名同学？
【题目】重庆市的重大惠民工程--公租房建设已陆续竣工，计划10年内解决低收入人群的住房问题，前6年，每年竣工投入使用的公租房面积
单位：百万平方米
，与时间x的关系是
单位：年， 
且x为整数
；后4年，每年竣工投入使用的公租房面积
单位：百万平方米
，与时间x的关系是
单位：年， 
且x为整数
假设每年的公租房全部出租完
另外，随着物价上涨等因素的影响，每年的租金也随之上调，预计，第x年投入使用的公租房的租金
单位：元
与时间
单位：年， 
且x为整数
满足一次函数关系如下表：
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
求出z与x的函数关系式；
求政府在第几年投入的公租房收取的租金最多，最多为多少百万元；
若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年投入的公租房总面积不变的情况下，要让人均住房面积比第6年人均住房面积提高
，这样可解决住房的人数将比第6年减少
，求a的值．
参考数据： 
