题目内容
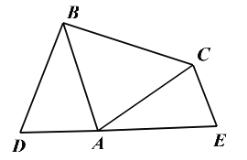
【题目】如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC·CE,AD=6,AE=4.
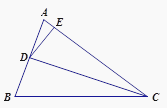
(1)求证:△BCD∽△DCE;
(2)求证:△ADE∽△ACD;
(3)求CE的长.
【答案】(1)证明见解析(2)证明见解析(3)5
【解析】试题分析:(1)根据两边对应成比例,且夹角相等的两个三角形相似,可得答案;
(2)根据两个角对应相等的两个三角形相似,可得答案;
(3)根据两个三角形相似,对应边成比例,可得答案.
试题解析:(1)证明:CD是△ABC中∠ACB的角平分线,
∴∠BCD=∠DCE.
∵CD2=BCCE,
∴![]() ,
,
∴△BCD∽△DCE(两边对应成比例,且夹角相等的两个三角形相似);
(2)证明:∵△BCD∽△DCE,
∴∠EDC=∠DBC(相似三角形的对应角相等).
∵∠ADC=∠DBC+∠DCB(三角形的外角等于与它不相邻的两个内角的和),
∠ADC=∠ADE+∠EDC,
∴∠ADE=∠ACD.
∠A=∠A,
∴△ADE∽△ACD(两个角对应相等的两个三角形相似);
(3)解:∵△ADE∽△ACD,
∴![]() ,
,
∴![]() ,
,
∴AC=9,
∴CE=AC-AE=9-4=5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少![]() .
.
A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格 | 1100 | 1400 |
销售价格 | 今年的销售价格 | 2000 |
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?