题目内容
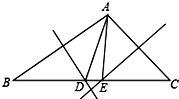
【题目】如图，在△ABC中， AB的垂直平分线交BC于D，AC的中垂线交BC于E，∠BAC=124°，则∠DAE的度数为( )
A.68°B.62°C.66°D.56°
【答案】A
【解析】
首先利用三角形内角和定理，求出∠B+∠C=180°-124°=56°，然后根据垂直平分线的性质得出∠B=∠BAD，∠C=∠CAE，进而得出∠BAD+∠CAE=∠B+∠C=56°，即可得解.
∵在△ABC中，∠BAC=124°
∴∠B+∠C=180°-124°=56°
又∵AB的垂直平分线交BC于D，AC的中垂线交BC于E，
∴∠B=∠BAD，∠C=∠CAE
∴∠BAD+∠CAE=∠B+∠C=56°
∴∠DAE=∠BAC-∠BAD-∠CAE=124°-56°=68°
故答案为A.
练习册系列答案
名校课堂系列答案
相关题目
【题目】随着人们生活水平的提高，家用轿车越来越多地进入家庭，小明家中买了一辆小轿车，他连续记录了
天中每天行驶的路程(如下表)，以
为标准，多于的记为“
”，不足的记为“
”，刚好的记为“
”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程 |
|
|
|
|
|
|
|
（1）请求出这天中平均每天行驶多少千米？
（2）若每行驶需用汽油
升，汽油价
元/升，计算小明家这天的汽油费用大约是多少元？
