Question

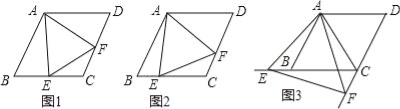
【题目】 已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE＝AP＝1，BP＝．下列结论：

①△APD≌△AEB；②点B到直线AE的距离为；

③S△APD+S△APB＝+；④S正方形ABCD＝4+．

其中正确结论的序号是_____．

Answer 1

【答案】①③④

【解析】

由题意可得△ABE≌△APD，故①正确，可得∠APD＝∠AEB＝135°，则∠PEB＝90°，由勾股定理可得BE，作BM⊥AE于M，可得△BEM是等腰直角三角形，

可得BM＝EM＝，故②错误，根据面积公式即可求S△APD+S△APB，S正方形ABCD，根据计算结果可判断．

解：∵正方形ABCD

∴AB＝AD，∠BAD＝90°

又∵∠EAP＝90°

∴∠BAE＝∠PAD，AE＝AP，AB＝AD

∴△AEB≌△APD故①正确

作BM⊥AE于M，

∵AE＝AP＝1，∠EAP＝90°

∴EP＝，∠APE＝45°＝∠AEP

∴∠APD＝135°

∵△AEP≌△APD，

∴∠AEB＝135°

∴∠BEP＝90°

∴BE

∵∠M＝90°，∠BEM＝45°

∴∠BEM＝∠EBM＝45°

∴BE＝MB 且BE＝,

∴BM＝ME＝,故②错误

∵S△APD+S△APB＝S四边形AMBP﹣S△BEM

故③正确

∵S正方形ABCD＝AB2＝AE2+BE2

∴S正方形ABCD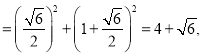 故④正确

∴正确的有①③④