Question

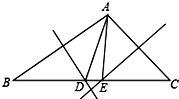
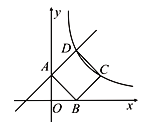
【题目】如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，点G是EF的中点，连接CG、BG、BD、DG，下列结论：① BC=DF，②∠DGF=135o；③BG⊥DG，④ 若3AD=4AB，则4S△BDG=25S△DGF；正确的是____________（只填番号）．

Answer 1

【答案】①③④

【解析】

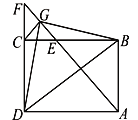
根据矩形的性质得：BC=AD，∠BAD=∠ADC=90°，由角平分线可得△ADF是等腰直角三角形，则BC=DF=AD，故①正确；

先求出∠BAE=45°，判断出△ABE是等腰直角三角形，根据等腰直角三角形的性质可得AB=BE，∠AEB=45°，从而得到BE=CD；再求出△CEF是等腰直角三角形，根据等腰直角三角形的性质可得CG=EG，再求出∠BEG=∠DCG=135°，然后利用“边角边”证明△BEG≌△DCG，得到∠BGE=∠DGC，由∠BGE＜∠AEB，得到∠DGC=∠BGE＜45°，∠DGF＜135°，故②错误；

由全等三角形的性质可得∠BGE=∠DGC，即可得到③正确；

由△BGD是等腰直角三角形得到BD=5a，求得S△BDG，过G作GM⊥CF于M，求得S△DGF，进而得出答案．

∵四边形ABCD是矩形，∴BC=AD，∠BAD=∠ADC=90°．

∵AF平分∠BAD，∴∠BAE=∠DAF=45°，∴△ADF是等腰直角三角形，∴DF=AD，∴BC=DF，故选项①正确；

∵AE平分∠BAD，∴∠BAE=45°，∴△ABE是等腰直角三角形，∴AB=BE，∠AEB=45°．

∵AB=CD，∴BE=CD；

∵∠CEF=∠AEB=45°，∠ECF=90°，∴△CEF是等腰直角三角形．

∵点G为EF的中点，∴CG=EG，∠FCG=45°，∴∠BEG=∠DCG=135°．

在△BEG和△DCG中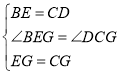，∵，∴△BEG≌△DCG（SAS），∴∠BGE=∠DGC．

∵∠BGE＜∠AEB，∴∠DGC=∠BGE＜45°．

∵∠CGF=90°，∴∠DGF＜135°，故②错误；

∵△BEG≌△DCG，∴∠BGE=∠DGC，BG=DG．

∵∠EGC=90°，∴∠BGD=90°，∴BG⊥DG，故③正确；

∵3AD=4AB，∴，∴设AB=3a，则AD=4a．

∵BD=5a，∴BG=DGa，∴S△BDGa2．

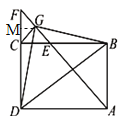
过G作GM⊥CF于M．

∵CE=CF=BC﹣BE=BC﹣AB=a，∴GMCFa，∴S△DGFDFGM4aa=a2，∴S△BDGS△DGF，∴4S△BDG=25S△DGF，故④正确．

故答案为：①③④．