题目内容
【题目】在如图所示的平面直角坐标系中,画出函数y=2x+4的图象;
(1)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(2)在(1)的条件下,求出△AOB的面积;
(3)利用图象直接写出:当y<0时,x的取值范围.
【答案】画出函数图像;(1)A(-2,0),B(0,4);(2)4;(3)x<-2.
【解析】
根据一次函数的图像画法,通过列表、描点、连线画图即可;(1)利用函数解析式分别代入x=0与y=0的情况就可以求出交点坐标;(2)根据点A、点B的坐标求得OA、OB的长,再利用三角形的面积公式求解即可;(3)根据图象直接求解即可.
函数y=2x+4的图象如图所示:
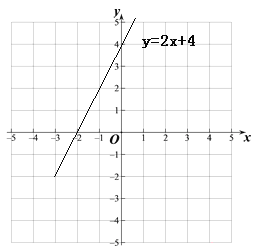
(1)∵函数y=2x+4与两个坐标轴的交点为(-2,0),(0,4),
∴A(-2,0) ,B(0,4);
(2)∵A(-2,0) ,B(0,4),
∴AO=2,BO=4,
∴S△ABO=4;
(3)由图象知,当x﹤-2时,y﹤0.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目