题目内容
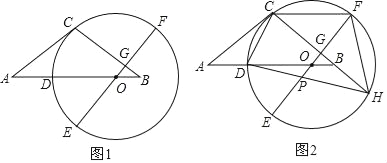
【题目】如图1，等腰△ABC中，AC=BC，点O在AB边上，以O为圆心的圆经过点C，交AB边于点D，EF为⊙O的直径，EF⊥BC于点G，且D是
的中点．
（1）求证：AC是⊙O的切线；
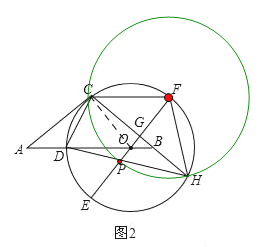
（2）如图2，延长CB交⊙O于点H，连接HD交OE于点P，连接CF，求证：CF=DO+OP；
（3）在（2）的条件下，连接CD，若tan∠HDC=
，CG=4，求OP的长．
【答案】（1）见解析；（2）见解析；（3）
【解析】试题分析： 
连接OC． 
得到
得出
即可证明AC是
的切线.
如图2中，连接OC，首先证明
再证明点P在以F为圆心FC为半径的圆上，即可解决问题；
在
中，利用
求出
根据勾股定理求得
在Rt 
中，根据勾股定理得， 
利用
中的结论即可求出
的长度.
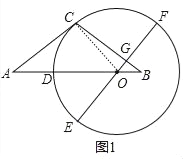
试题解析：（1）证明：如图1中，连接OC．
∵
∴
∵
∴
∴
∵点D是
的中点，
∴
=
,
∴
∴
∴
∴
∴AC是
的切线，
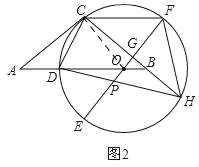
（2）证明：如图2中，连接OC，
∵
∴
∴EF垂直平分HC，
∴
∵
∵
∴
∵
∴
∴点P在以F为圆心FC为半径的圆上，
∴
∵
∴
即
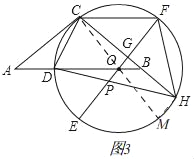
（3）如图3，连接CO并延长交
于M，连接
，
∴
∵
于G，
在
中， 
∴
∴
∴
∴
∵
∴OG∥MH，
∵
∴
∴
在Rt 
中，根据勾股定理得， 
由（2）知， 
【题目】2018年3月，某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动，活动结束后，随机抽取了部分同学的成绩（x均为整数，总分100分），绘制了如下尚不完整的统计图表．
调查结果统计表
组别 | 成绩分组（单位：分） | 频数 | 频率 |
A | 80≤x＜85 | 50 | 0.1 |
B | 85≤x＜90 | 75 | |
C | 90≤x＜95 | 150 | c |
D | 95≤x≤100 | a | |
合计 | b | 1 |
根据以上信息解答下列问题：
（1）统计表中，a=_____，b=_____，c=_____；
（2）扇形统计图中，m的值为_____，“C”所对应的圆心角的度数是_____；
（3）若参加本次竞赛的同学共有5000人，请你估计成绩在95分及以上的学生大约有多少人？
