题目内容
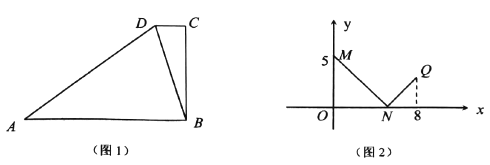
【题目】已知:梯形![]() 中,
中,![]() ,联结
,联结![]() (如图1). 点
(如图1). 点![]() 沿梯形的边从点
沿梯形的边从点![]() 移动,设点
移动,设点![]() 移动的距离为
移动的距离为![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 从点
从点![]() 移动到点
移动到点![]() 时,
时,![]() 与
与![]() 的函数关系(如图2)中的折线
的函数关系(如图2)中的折线![]() 所示. 试求
所示. 试求![]() 的长;
的长;
(3)在(2)的情况下,点![]() 从点
从点![]() 移动的过程中,
移动的过程中,![]() 是否可能为等腰三角形?若能,请求出所有能使
是否可能为等腰三角形?若能,请求出所有能使![]() 为等腰三角形的
为等腰三角形的![]() 的取值;若不能,请说明理由.
的取值;若不能,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 或
或![]()
【解析】
(1)由平行线的性质、直角三角形的性质、等腰三角形的性质得出∠ABD=∠CDB,∠A+∠ADC=180°,∠ABD+∠CBD=90°,∠ABD=∠ADB,得出∠A+2∠ABD=180°,2∠ABD+2∠CBD=180°,即可得出结论;
(2)作DE⊥AB于E,则DE=BC=3,CD=BE,由勾股定理求出AE=![]() =4,得出CD=BE=AB-AE=1;
=4,得出CD=BE=AB-AE=1;
(3)分情况讨论:①点P在AB边上时;②点P在BC上时;③点P在AD上时;由等腰三角形的性质和勾股定理即可得出答案.
(1)证明:∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,即
,即![]()
∴![]()
(2)解:由点![]() ,得
,得![]() ,
,
由点![]() 点的横坐标是8,得
点的横坐标是8,得![]() 时,∴
时,∴![]()
作![]() 于
于![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]()
(3)
情况一:点![]() 在
在![]() 边上,作
边上,作![]() ,
,
当![]() 时,
时,![]() 是等腰三角形,此时,
是等腰三角形,此时,![]() ,
,
∴![]()
情况二:点![]() 在
在![]() 边上,当
边上,当![]() 时
时![]() 是等腰三角形,
是等腰三角形,
此时,![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
即![]() ,
,
∴![]()
情况三:点![]() 在
在![]() 边上时,
边上时,![]() 不可能为等腰三角形
不可能为等腰三角形
情况四:点![]() 在
在![]() 边上,有三种情况
边上,有三种情况
1°作![]() ,当
,当![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,
此时,∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
2°当![]() 时
时![]() 为等腰三角形,
为等腰三角形,
此时,![]()
3°当点![]() 与点
与点![]() 重合时
重合时![]() 为等腰三角形,
为等腰三角形,
此时![]() 或
或![]() .
.

练习册系列答案
相关题目