题目内容
【题目】如图，小华剪了两条宽为1的纸条，交叉叠放在一起，且它们较小的交角为60°，则它们重叠部分的面积为（ ）
A. 3 B. 2 C. 
D. 
【答案】D
【解析】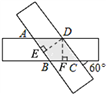
过点D作DE⊥AB，垂足为E；过点D作DF⊥BC，垂足为F. (如图)
根据辅助线作法和纸条宽度的定义可知：∠AED=∠CFD=90°，DE=DF=1，
由纸条的几何特征可知，AD∥BC，AB∥DC，故四边形ABCD为平行四边形，
由题目条件和对顶角关系可知，∠BCD=60°，
∴在平行四边形ABCD中，∠BAD=∠BCD=60°，即∠EAD=∠FCD=60°，
∵在△AED与△CFD中：
，
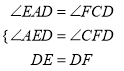∴△AED≌△CFD (AAS)
∴AD=CD，
∴平行四边形ABCD为菱形，
∵在Rt△CFD中，∠FCD=60°，
∴∠FDC=30°，
∴在Rt△CFD中， 
，
∴在Rt△CFD中， 
，
∴
，
∵在菱形ABCD中，BC=CD，
∴
，
∴菱形ABCD的面积为： 
，即纸片重叠部分的面积为
.
故本题应选D.
练习册系列答案
相关题目
