题目内容
【题目】已知△ABC是等边三角形，点D，E分别为边AB，AC上的点，且有AE＝DB，连接DE，DC．
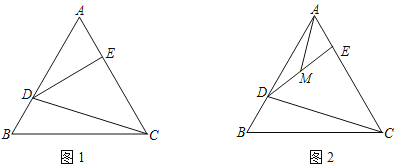
（1）如图1，若AB＝6，∠DEC＝90°，求△DEC的面积．
（2）M为DE中点，当D，E分别为AB、AC的中点时，判定CD，AM的数量关系并说明理由．
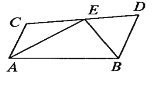
（3）如图2，M为DE中点，当D，E分别为AB，AC上的动点时，判定CD，AM的数量关系并说明理由．
【答案】（1）S△DEC＝4
；（2）CD＝2AM．理由见解析；（3）CD＝2AM．理由见解析.
【解析】
（1）如图1中，设AE=BD=x．证明AD=2AE=2x，构建方程求出x即可解决问题；
（2）利用等边三角形的性质判断出CD与BC的关系，再判断出△ADE是等边三角形，进而判断出AM与BC关系即可得出结论；
（3）先判断出△BDF是等边三角形，进而得出四边形ADFE是平行四边形，再利用全等三角形的性质得出AF=CD即可得出结论.
（1）如图1中，设AE＝BD＝x．
∵△ABC是等边三角形，
∴∠A＝60°，
∵∠DEC＝∠AED＝90°，
∴∠ADE＝30°，
∴AD＝2AE＝2x，DE＝AE＝x，
∵AB＝6，
∴x+2x＝6，
∴x＝2，
∴AE＝2，EC＝4，DE＝2，
∴S△DEC＝
DEEC＝×2×4＝4．
（2）结论：CD＝2AM．
理由：如图2中，
∵AB＝AC，∠BAC＝60°，
∴△ABC是等边三角形，
∵点D是AB的中点，
∴CD＝
BC，
∵点D，E是AB，AC的中点，
∴AD＝AB，AE＝AC，
∴AD＝AE，
∵∠BAC＝60°，
∴△ADE是等边三角形，
∵点M是DE的中点，
∴AM＝AD＝
AB＝BC，
∴CD＝2AM，
故答案为：CD＝2AM，
（3）结论：CD＝2AM．
理由：如图2中，过点D作DF∥AC交BC于F，连接EF，AF．
∴∠BDF＝∠BAC＝60°，
∵AB＝AC，∠BAC＝60°，
∴△ABC是等边三角形，
∴∠ABC＝60°，
∴△BDF是等边三角形，
∴DF＝BD，
∵BD＝AE，
∴DF＝AE，
∵DF∥AE，
∴四边形ADFE是平行四边形，
∴AF必过DE的中点，
∵点M是DE的中点，
∴AF过DE的中点，
∴AF＝2AM，
在△ABF和△CBD中，
，
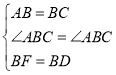∴△ABF≌△CBD（SAS），
∴AF＝CD，
∴CD＝2AM.
