题目内容
【题目】数学复习课上，张老师出示了下框中的问题：
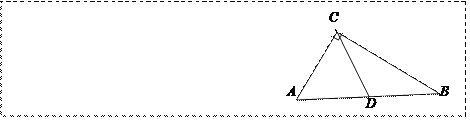
已知：在Rt△ACB中，∠C＝90°，点D是斜边AB上的中点，连接CD.
求证：CD＝
AB.
问题思考
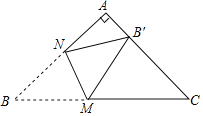
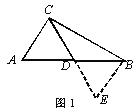
（1）经过独立思考，同学们想出了多种正确的证明思想，其中有位同学的思路如下：如图1，过点B作BE∥AC交CD的延长线于点E。请你根据这位同学的思路提示证明上述框中的问题.
方法迁移
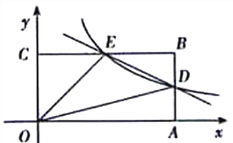
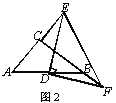
（2）如图2，在Rt△ACB中，∠ACB＝90°，点D为AB的中点，点E是线段AC上一动点，连接DE，线段DF始终与DE垂直且交BC于点F。试猜想线段AE，EF，BF之间的数量关系，并加以证明.
拓展延伸
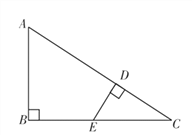
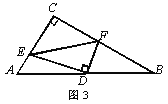
（3）如图3，在Rt△ACB中，∠ACB＝90°，点D为AB的中点，点E是线段AC延长线上一动点，连接DE，线段DF始终与DE垂直且交CB延长线于点F。试问第（2）小题中线段AE，EF，BF之间的数量关系会发生改变吗？若会，请写出关系式；若不会，请说明理由.
【答案】（1）CD=
AB；（2）AE2+BF2=EF2；(3)线段AE、EF、FB的数量关系不会发生改变，仍有AE2+BF2=EF2.
【解析】分析：（1）证ΔACD≌ΔBED和△ACB≌△EBC得证；
（2）如图2，过B作BG∥AC交ED延长线于G，连接GF.通过证ΔADE≌ΔBDG和在Rt△BFG中，得到AE2+BF2=EF2.
（3）如图3，过A作AG//BC交FD的延长线于点G，连接EG，类似（2）问，通过证ΔADG≌ΔBDF，将AE、BF、EF移至Rt△AEG中，可得AE2+BF2=EF2.
详解：(1)证明:∵在⊿ABC中，∠C=90°，D是斜边AB中点，
过B作BE//AC交CD延长线于E，
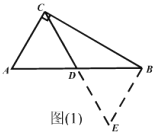
∴∠CAB=∠ABE, ∠ACE=∠BEC，
∴⊿ADC∽⊿BDE，∴D为CE中点，
∵∠CAB+∠CBA=90°，∠ABE+∠CBA=90°，
∴⊿ABC≌⊿ECB，AB=CE，
∴CD=AB.
(2)证明:过B作BG//AC交ED延长线于G，连接GF.
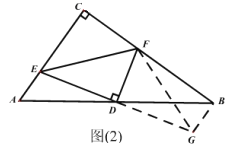
∴∠EAD=∠GBD，又∠EDA=∠GDB，AD=DB，
∴ΔAED≌ΔBDG，∴AE=BG，DE=DG，
又∵DF⊥DE，∴DF是EG中垂线，EF=GF，
∵∠C=90，∠GBF=90，∴BF2+BG2=GF2;
∴AE2+BF2=EF2.
(3)线段AE、EF、FB的数量关系不会发生改变，仍有AE2+BF2=EF2.
证明:如图3，过A作AG//BC交FD的延长线于点G，连接EG，
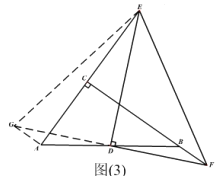
∵AG//BC，∴∠GAD＝∠DBF，∠AGD＝∠DFB，
∵点D为AB的中点，∴AD＝DB，
∴⊿ADG≌⊿BDF，∴AG=BF，GD＝DF，
∵DE⊥DF，∴EF＝EG，
∵AG//BC，∠EAG＝∠ACB＝90°，
∴AE2＋AG2＝EG2，
∴AE2+BF2=EF2.
