题目内容
【题目】定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min{2,﹣4}=﹣4,min{1,5}=1,则min{﹣x2+1,﹣x}的最大值是_________.
【答案】![]() .
.
【解析】分析:理解min{a,b}的含义就是取二者中的较小值,画出函数图象草图,利用函数图象的性质可得结论.
详解:在同一坐标系xOy中,画出函数二次函数y=﹣x2+1与正比例函数y=﹣x的图象,如图所示.设它们交于点A、B.
令﹣x2+1=﹣x,即x2﹣x﹣1=0,解得:x=![]() 或
或![]() ,
,
∴A(![]() ),B(
),B(![]() ).
).
观察图象可知:
①当x≤![]() 时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而增大,其最大值为
时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而增大,其最大值为![]() ;
;
②当![]() <x<
<x<![]() 时,min{﹣x2+1,﹣x}=﹣x,函数值随x的增大而减小,其最大值为
时,min{﹣x2+1,﹣x}=﹣x,函数值随x的增大而减小,其最大值为![]() ;
;
③当x≥![]() 时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而减小,最大值为
时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而减小,最大值为![]() .
.
综上所示,min{﹣x2+1,﹣x}的最大值是![]() .
.
故答案:![]() .
.
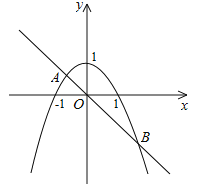

练习册系列答案
相关题目