题目内容
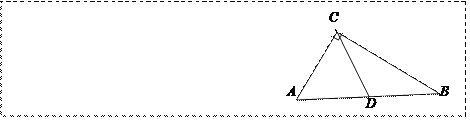
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=![]() +1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_______.
+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_______.
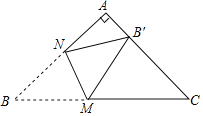
【答案】![]()
![]() +
+![]() ,1
,1
【解析】
①如图1,当∠B′MC=90°,B′与A重合,M是BC的中点,于是得到结论;②如图2,当∠MB′C=90°,推出△CMB′是等腰直角三角形,得到CM=![]() MB′,列方程即可得到结论.
MB′,列方程即可得到结论.
①如图1,
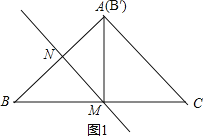
当∠B′MC=90°,B′与A重合,M是BC的中点,
∴BM=![]() BC=
BC=![]()
![]() +
+![]() ;
;
②如图2,当∠MB′C=90°,
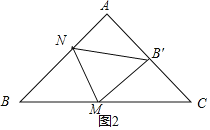
∵∠A=90°,AB=AC,
∴∠C=45°,
∴△CMB′是等腰直角三角形,
∴CM=![]() MB′,
MB′,
∵沿MN所在的直线折叠∠B,使点B的对应点B′,
∴BM=B′M,
∴CM=![]() BM,
BM,
∵BC=![]() +1,
+1,
∴CM+BM=![]() BM+BM=
BM+BM=![]() +1,
+1,
∴BM=1,
综上所述,若△MB′C为直角三角形,则BM的长为![]()
![]() +
+![]() 或1,
或1,
故答案为:![]()
![]() +
+![]() 或1.
或1.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目