题目内容
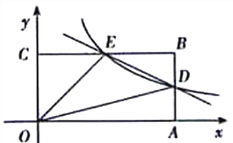
【题目】如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都
在坐标轴上,点B的坐标是(4.2),反比例函数![]() 与AB,BC分别交于点D,E。
与AB,BC分别交于点D,E。
(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。
【答案】(1)![]() . (2)F的坐标为(0,3)或(0,-3).
. (2)F的坐标为(0,3)或(0,-3).
【解析】试题分析:(1)先求出D、E的坐标,然后用待定系数法即可求出直线的解析式;
(2)先求出△ODE的面积,然后由△OEF和△ODE的面积相等,求出OF的长,即可得到结论.
试题解析:解:(1)由B(4,2)知,点D的横坐标是4,点E的纵坐标是2,
又∵点D,E都在![]() 的图象上,∴D(4,1),E(2,2).
的图象上,∴D(4,1),E(2,2).
设直线DE的解析式为![]() ,把D(4,1),E(2,2)代入,得:
,把D(4,1),E(2,2)代入,得:
![]() 解得:
解得: 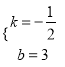
∴直线DE的解析式为![]() .
.
(2)∵D(4,1),E(2,2),B(4,2),
∴S△ODE= S矩形OABC - S△OCE - S△BDE- S△OAD![]() =3.
=3.
∵点F为y轴上一点,S△OEF=S△ODE,
∴S△OEF![]() .
.
∴OF=3.
∴F的坐标为(0,3)或(0,-3).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目