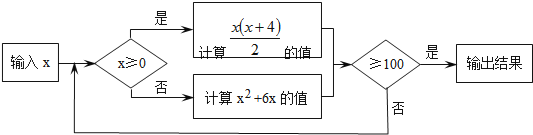
题目内容
【题目】一只不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同．
（1）搅匀后，从中任意摸出一个球，恰好是红球的概率是 ；
（2）搅匀后，从中任意摸出一个球，记录颜色后放回、搅匀，再从中任意摸出一个球．
①求两次都摸到红球的概率；
②经过了n次“摸球﹣记录﹣放回”的过程，全部摸到红球的概率是 ．
【答案】（1）
；（2）①P（B）=
；②（ 
）n．
【解析】试题分析：
（1）由题意易可知，共有3种等可能结果，其中是红球的占了2种，由此可得所求概率为
；
（2）①画树状图分析出所有的等可能结果，看其中两次都是红球的有多少种，即可得到所求概率；②由题意可知，摸一次有3种等可能结果，放回摸第2次后共有9种等可能结果，……，摸n次后共有
个等可能结果，其中全是红球的有
种，由此即可得到所求概率.
试题解析：
（1）∵一只不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同，
∴搅匀后，从中任意摸出一个球，恰好是红球的概率是： 
；
故答案为： 
．
（2）①画树状图得：
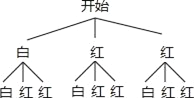
∵共有9种，它们出现的可能性相同．所有的结果中，满足“两次都是红球”（记为事件B）的结果只有4种，
P（B）=
；
②∵经过了n次“摸球﹣记录﹣放回”的过程，共有3n种等可能的结果，全部摸到红球的有2n种情况，
∴全部摸到红球的概率是：（
）n．
故答案为：（
）n．
练习册系列答案
相关题目
