题目内容
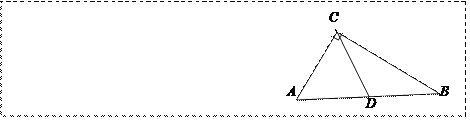
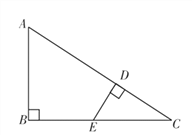
【题目】如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰.已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?
【答案】2-![]()
【解析】整体分析:
设相遇时补给船航行了x海里,在Rt△CDE中,用含x的代数式表示出DE,CE,由勾股定理列方程求解.
解:设相遇时补给船航行了x海里,即DE=x海里
∵军舰的速度是补给船的2倍,他们的时间相同,
∴AB+BE=2x.
∵AB+BC=3,
∴EC=3-2x.
Rt△CDE中,CD=1,
根据勾股定理可得方程
x2+12=(3-2x)2.
解得x1=2-![]() ,x2=2+
,x2=2+![]() (不合题意,舍去).
(不合题意,舍去).
答:相遇时补给船航行了(2-![]() )海里
)海里

练习册系列答案
相关题目