题目内容
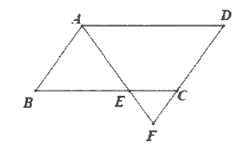
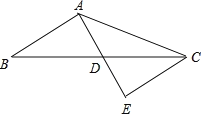
【题目】如图，在△ABC中，AB=6，AC=10，AD是BC边上的中线，且AD=4，延长AD到点E，使DE=AD，连接CE．
(1)求证：△AEC是直角三角形．
(2)求BC边的长．
【答案】(1)证明见解析；(2)BC=
．
【解析】
（1）首先证明△ABD≌△ECD，推出EC=AB=6，由AE2+EC2=AC2，推出△AEC是直角三角形．
（2）在Rt△CDE中，求出CD，根据BC=2CD即可解决问题．
(1)∵AD是BC边上的中线
∴BD=CD
又∵DE=AD, ∠ADB=∠CDE
∴△ABD≌△ECD，
∴EC=AB=6，
∵AE=8 ，AC=10
∴△AEC 中，AE2+EC2=AC2
∴△AEC是直角三角形．
(2)在Rt△CDE中，CD2=CE2+DE2=62+42=52
∴CD=
∴BC=2CD=．
【题目】在学校组织的“学习强国”知识竞赛中，每班参加比赛的人数相同，成绩分为
，
，
，
四个等级其中相应等级的得分依次记为
分，
分，
分和
分.年级组长张老师将
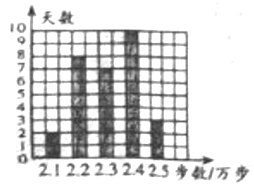
班和
班的成绩进行整理并绘制成如下的统计图：
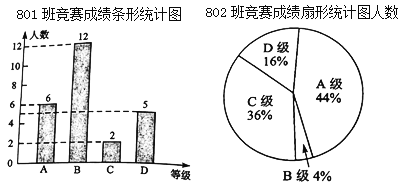
（1）在本次竞赛中，班级的人数有多少。
（2）请你将下面的表格补充完整：
成绩 班级 | 平均数（分） | 中位数 （分） | 众数 （分） | B级及以上人数 |
|
|
|
| |
|
|
|
（3）结合以上统计量，请你从不同角度对这次竞赛成绩的结果进行分析（写出两条）
【题目】某公司购进某种矿石原料300吨，用于生产甲、乙两种产品，生产1吨甲产品或1吨乙产品所需该矿石和煤原料的吨数如下表:
产品资源 | 甲 | 乙 |
矿石（吨） | 10 | 4 |
煤（吨） | 4 | 8 |
生产1吨甲产品所需成本费用为4000元，每吨售价4600元；
生产1吨乙产品所需成本费用为4500元，每吨售价5500元，
现将该矿石原料全部用完，设生产甲产品x吨，乙产品m吨，公司获得的总利润为y元.
（1）写出m与x之间的关系式
（2）写出y与x之间的函数表达式，并写出自变量的范围
（3）若用煤不超过200吨，生产甲产品多少吨时，公司获得的总利润最大，最大利润是多少？
