题目内容
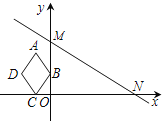
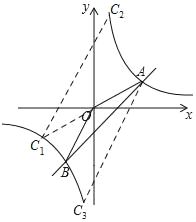
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

【答案】(1)y=![]() ,y=x﹣1;(2)x<﹣2或0<x<3时,直线AB在双曲线的下方;(3)存在点C,点C的坐标为(﹣3,﹣2),(
,y=x﹣1;(2)x<﹣2或0<x<3时,直线AB在双曲线的下方;(3)存在点C,点C的坐标为(﹣3,﹣2),(![]() ,
, ![]() ),(﹣
),(﹣![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)设反比例函数解析式为y=![]() ,将B点坐标代入,求出反比例函数解析式,将A点坐标代入反比例解析式求出m的值,确定出点A的坐标,设直线AB 的解析式为y=ax+b,将A与B的坐标代入一次函数解析式求出a与b的值,即可确定出一次函数解析式;
,将B点坐标代入,求出反比例函数解析式,将A点坐标代入反比例解析式求出m的值,确定出点A的坐标,设直线AB 的解析式为y=ax+b,将A与B的坐标代入一次函数解析式求出a与b的值,即可确定出一次函数解析式;
(2)根据图像写出答案即可;
(3)分3中情况求解,延长AO交双曲线于点C1,由点A与点C1关于原点对称,求出点点C1的坐标;如图,过点C1作BO的平行线,交双曲线于点C2,将OB的解析式与C1C2的解析式联立,求出点C2的坐标;A作OB的平行线,交双曲线于点C3,,将AC3的解析式与反比例函数的解析式联立,求出点C3的坐标
解:(1)设反比例函数解析式为y=![]() ,
,
把B(﹣2,﹣3)代入,可得k=﹣2×(﹣3)=6,
∴反比例函数解析式为y=![]() ;
;
把A(3,m)代入y=![]() ,可得3m=6,
,可得3m=6,
即m=2,
∴A(3,2),
设直线AB 的解析式为y=ax+b,
把A(3,2),B(﹣2,﹣3)代入,可得![]() ,
,
解得![]() ,
,
∴直线AB 的解析式为y=x﹣1;
(2)由题可得,当x满足:x<﹣2或0<x<3时,直线AB在双曲线的下方;
(3)存在点C.
如图所示,延长AO交双曲线于点C1,
∵点A与点C1关于原点对称,
∴AO=C1O,
∴△OBC1的面积等于△OAB的面积,
此时,点C1的坐标为(﹣3,﹣2);
如图,过点C1作BO的平行线,交双曲线于点C2,则△OBC2的面积等于△OBC1的面积,
∴△OBC2的面积等于△OAB的面积,
由B(﹣2,﹣3)可得OB的解析式为y=![]() x,
x,
可设直线C1C2的解析式为y=![]() x+b',
x+b',
把C1(﹣3,﹣2)代入,可得﹣2=![]() ×(﹣3)+b',
×(﹣3)+b',
解得b'=![]() ,
,
∴直线C1C2的解析式为y=![]() x+
x+![]() ,
,
解方程组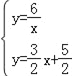 ,可得C2(
,可得C2(![]() ,
,![]() );
);
如图,过A作OB的平行线,交双曲线于点C3,则△OBC3的面积等于△OBA的面积,
设直线AC3的解析式为y=![]() x+
x+ ![]() ,
,
把A(3,2)代入,可得2=![]() ×3+
×3+ ![]() ,
,
解得![]() =﹣
=﹣![]() ,
,
∴直线AC3的解析式为y=![]() x﹣
x﹣![]() ,
,
解方程组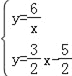 ,可得C3(﹣
,可得C3(﹣![]() ,﹣
,﹣![]() );
);
综上所述,点C的坐标为(﹣3,﹣2),(![]() ,
,![]() ),(﹣
),(﹣![]() ,﹣
,﹣![]() ).
).

 智慧小复习系列答案
智慧小复习系列答案【题目】八年级380名师生参加户外拓展活动,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用乙种客车x辆,租车总费用为y元求出y(元)与x(辆)之间的函数表达式;
(2)当乙种客车租用多少辆时,能保障所有的师生能参加户外拓展活动且租车费用最少,最少费用是多少元?