题目内容
【题目】在ABCD中,点E,F分别在边BC,AD上,且AF=CE.

(Ⅰ)如图①,求证四边形AECF是平行四边形;
(Ⅱ)如图②,若∠BAC=90°,且四边形AECF是边长为6的菱形,求BE的长.
【答案】(1)证明见解析;(2)6.
【解析】
(I)根据平行四边形的性质得出AD∥BC,根据平行四边形的判定推出即可;
(II)根据菱形的性质求出AE=6,AE=EC,求出AE=BE即可.
(I)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=CE,
∴四边形AECF是平行四边形;
(II)如图:
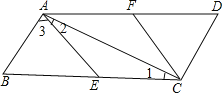
∵四边形AECF是菱形,
∴AE=EC,
∴∠1=∠2,
∵∠BAC=90°,
∴∠2+∠3=90°∠1+∠B=90°,
∴∠3=∠B,
∴AE=BE,
∵AE=6,
∴BE=6.

【题目】定向越野作为一种新兴的运动项目,深受人们的喜爱. 这种定向运动是利用地图和指北针到访地图上所指示的各个点标,以最短时间按序到达所有点标者为胜. 下面是我区某校进行定向越野活动中,中年男子组的成绩(单位:分:秒).
9:01 14:45 9:46 19:22 11:20 18:47 11:40 12:32 11:52 13:45
22:27 15:00 17:30 13:22 18:34 10:45 19:24 16:26 21:33 15:31
19:50 14:27 15:55 16:07 20:43 12:13 21:41 14:57 11:39 12:45
12:57 15:31 13:20 14:50 14:57 9:41 12:13 14:27 12:25 12:38
例如,用时最少的赵老师的成绩为9:01,表示赵老师的成绩为9分1秒.

以下是根据某校进行定向越野活动中,中年男子组的成绩中的数据,绘制的统计图表的一部分.
某校中年男子定向越野成绩分段统计表
分组/分 | 频数 | 频率 |
9≤x<11 | 4 | 0.1 |
11≤x<13 | b | 0.275 |
13≤x<15 | 9 | 0.225 |
15≤x<17 | 6 | d |
17≤x<19 | 3 | 0.075 |
19≤x<21 | 4 | 0.1 |
21≤x<23 | 3 | 0.075 |
合计 | a | c |
(1)这组数据的极差是____________;
(2)上表中的a =____________ ,b =____________ , c =____________, d =____________;
(3)补全频数分布直方图.