题目内容
【题目】在平行四边形ABCD中E是BC边上一点，且AB=AE，AE，DC的延长线相交于点F.
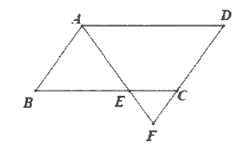
(1)若∠F=62°，求∠D的度数;
(2)若BE=3EC，且△EFC的面积为1，求平行四边形ABCD的面积.
【答案】（1）
（2）
【解析】
（1）由四边形ABCD是平行四边形，∠F=62°，易求得∠BAE的度数，又由AB=BE，即可求得∠B的度数，然后由平形四边形的对角相等，即可求得∠D的度数；
（2）根据相似三角形的性质求出△FEC与△FAD的相似比，得到其面积比，再找到△FEC与平行四边形的关系，求出平行四边形的面积．
（1）∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠BAF=∠F=62°，
∵AB=BE，
∴∠AEB=∠BAE=62°，
∴∠B=180°-∠BAE-∠AEB=56°，
∵在平行四边形ABCD中，∠D=∠B，
∴∠D=56°．
（2）∵DC∥AB，
∴△CEF∽△BEA．
∵BE=3EC
∴
，
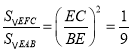∵S△EFC=1．
∴S△ABE=9a，
∵
∴
∴
∴
∵
∴
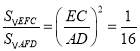
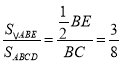
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
