题目内容
【题目】某公司购进某种矿石原料300吨,用于生产甲、乙两种产品,生产1吨甲产品或1吨乙产品所需该矿石和煤原料的吨数如下表:
产品资源 | 甲 | 乙 |
矿石(吨) | 10 | 4 |
煤(吨) | 4 | 8 |
生产1吨甲产品所需成本费用为4000元,每吨售价4600元;
生产1吨乙产品所需成本费用为4500元,每吨售价5500元,
现将该矿石原料全部用完,设生产甲产品x吨,乙产品m吨,公司获得的总利润为y元.
(1)写出m与x之间的关系式
(2)写出y与x之间的函数表达式,并写出自变量的范围
(3)若用煤不超过200吨,生产甲产品多少吨时,公司获得的总利润最大,最大利润是多少?
【答案】(1)m=75-2.5x;(2)y=-1900x+75000(0≤x≤30);(3)生产甲产品25吨时,公司获得的总利润最大,最大利润是27500元.
【解析】
(1)∵生产甲产品x吨,则用矿石原料10x吨.∴生产乙产品用矿石原料为(300-10x)吨,由此得出![]() ;
;
(2)先求出生产1吨甲、乙两种产品各获利多少,然后可求出获得的总利润.
(3)由于总利润y是x的一次函数,先求出x的取值范围,再根据一次函数的增减性,求得最大利润.
(1)m与x之间的关系式为
![]()
(2)生产1吨甲产品获利:4600-4000=600
生产1吨乙产品获利:5500-4500=1000
y与x的函数表达式为:![]() (0≤x≤30)
(0≤x≤30)
(3)根据题意列出不等式
![]()
解得x≥25
又∵0≤x≤30
∴25≤x≤30
∵y与x的函数表达式为:y=-1900x+75000
y随x的增大而减小,
∴当生产甲产品25吨时,公司获得的总利润最大
y最大=-1900×25+75000=27500(元).

【题目】我国每年的总用水主要包括四大方面:农业用水、工业用水、生活用水、其他用水. 2017年,我国农业用水量约![]() 亿
亿![]() (占总用水量的
(占总用水量的![]() ),工业用水量约为
),工业用水量约为![]() 亿
亿![]() ,生活用水量具体见下表.
,生活用水量具体见下表.
2019-2017年全国生活用水量表(单位:亿![]() )
)
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
用水量 |
|
|
|
|
|
|
|
|
|
(1)2017年全国总用水量约为 亿![]() ,其他用水约为 亿
,其他用水约为 亿![]() .
.
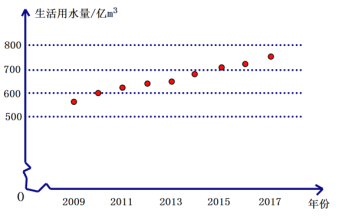
(2)根据“2019-2017年全国生活用水量表”,在平面直角坐标系中描出表中各对数值所对应的点(其中横坐标表示年份,纵坐标表示用水量)可发现,这些点近似的落在某条直线上.
①用靠近尽可能多点的直线来表示用水量的这种趋势,请在上图中画出这条直线;
②根据所画的直线,估计2018年全国生活用水量,并说明理由.
【题目】张先生今年7月份第一个星期的星期五以每股(份)25元的价格买进某种金融理财产品共2000股(买入时免收手续费),该理财产品在第二个星期的五个交易日中,每股的涨跌情况如下表(表格中数据表示比前一交易日涨或跌多少元) (单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌额 |
|
|
|
|
|
(1)写出第二个星期每日每股理财产品的收盘价(即每日最后时刻的成交价);
(2)已知理财产品卖出时,交易所需收取千分之三的手续费,如果张先生在第二个星期的星期五交易结束前将全部产品卖出,他的收益情况如何?