题目内容
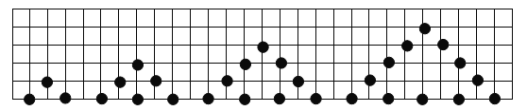
【题目】如图，用棋盘摆出下列一组三角形，三角形每边有
枚棋子，每个三角形的棋子总数是
.
（1）求
时
；
（2）按此规律推断，当三角形边上有枚棋子时，该三角形的棋子总数 （用含的代数式表示）；
（3）当三角形一边上有25枚棋子时，该三角形的棋子总数等于多少？
（4）当三角形的棋子总数是123枚时，该三角形一边上的棋子数是多少？
【答案】（1）15;（2）
;（3）S=72;（4）
.
【解析】
（1）仔细观察图形，然后分析三角形边上棋子的个数和棋子总数的个数，可得三角形边上每增加1枚棋子时，棋子总数增加3个，不难得出答案；
（2）根据变化规律写出S关于n的关系式即可；
（3）将n=25代入（2）中的关系式可得结果；
（4）将S=123代入（2）中关系式可得结果；
解：（1）当n=2时，
，
当n=3时，
，
当n=4时，
，
当n=5时，
，
当n=6时，
，
故答案为：15；
（2）按照（1）的规律可得：当三角形边上有
枚棋子时，该三角形的棋子总数
，
故答案为：；
（3）当n=25时，
；
（4）当S=123时，
，解得
.
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
【题目】八年级380名师生参加户外拓展活动,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表
甲种客车 | 乙种客车 | |
载客量（座/辆） | 60 | 45 |
租金（元/辆） | 550 | 450 |
(1)设租用乙种客车x辆,租车总费用为y元求出y(元)与x(辆)之间的函数表达式;
(2)当乙种客车租用多少辆时,能保障所有的师生能参加户外拓展活动且租车费用最少，最少费用是多少元?
【题目】20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准偏差 | －3 | －2 | －1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中，最重的一筐与最轻的一筐相差多少千克？
(2)这20筐白菜的平均质量比标准质量多或少多少千克？
(3)若白菜每千克售价2元，则出售这20筐白菜可卖多少元？
