Question

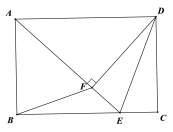
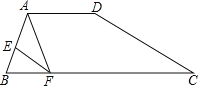
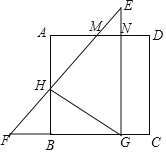
【题目】将正方形ABCD与等腰直角三角形EFG如图摆放，若点M、N刚好是AD的三等分点，下列结论正确的是（　　）

①△AMH≌△NME；②；③GH⊥EF；④S△EMN：S△EFG＝1：16

A.①②③④B.①②③C.①③④D.①②④

Answer 1

【答案】A

【解析】

利用三角形全等和根据题目设未知数，列等式解答即可.

解：设AM＝x，

∵点M、N刚好是AD的三等分点，

∴AM＝MN＝ND＝x，

则AD＝AB＝BC＝3x，

∵△EFG是等腰直角三角形，

∴∠E＝∠F＝45°，∠EGF＝90°，

∵四边形ABCD是正方形，

∴∠A＝∠ABC＝∠BGN＝∠ABF＝90°，

∴四边形ABGN是矩形，

∴∠AHM＝∠BHF＝∠AMH＝∠NME＝45°，

∴△AMH≌△NMH（ASA），故①正确；

∵∠AHM＝∠AMH＝45°，

∴AH＝AM＝x，

则BH＝AB﹣AH＝2x，

又Rt△BHF中∠F＝45°，

∴BF＝BH＝2x，＝，故②正确；

∵四边形ABGN是矩形，

∴BG＝AN＝AM＋MN＝2x，

∴BF＝BG＝2x，

∵AB⊥FG，

∴△HFG是等腰三角形，

∴∠FHB＝∠GHB＝45°，

∴∠FHG＝90°，即GH⊥EF，故③正确；

∵∠EGF＝90°、∠F＝45°，

∴EG＝FG＝BF＋BG＝4x，

则S△EFG＝EGFG＝4x4x＝8x2，

又S△EMN＝ENMN＝xx＝x2，

∴S△EMN：S△EFG＝1：16，故④正确；

故选A．